OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Baricentar
Koncept baricentra (težišta) prvi je uveo Arhimed iz Sirakuze u trećem veku pre nove ere. On je začetnik matematičkih tehnika koje su prve dovele do izračunavanja baricentara trougla, polusfere i eliptičkog paraboloida. Izučavanje baricentara je uveliko pomoglo da se razjasne razni problemi u astronomiji vezani za kretanje planeta u svojim sistemima, između ostalog i uticaj Meseca na Zemlju odnosno njeno kretanje u Sunčevom sistemu.
Masa Meseca, iako 81,3 puta manja od mase Zemlje, nije zanemarljiva.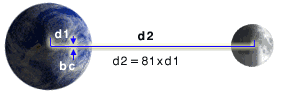 Ona deluje na Zemlju i zapravo Mesec ne kruži oko Zemlje, već Mesec i
Zemlja osciliraju oko jedne zajedničke tačke, oko zajedničkog centra mase
koji se zove baricentar. I zapravo tačka u kojoj se nalazi baricentar
obilazi Sunce po eliptičnoj putanji dok centri Meseca i Zemlje osciliraju
oko te tačke. Stoga ni putanja Meseca ni putanja Zemlje nemaju pravilan
eliptični oblik.
Ona deluje na Zemlju i zapravo Mesec ne kruži oko Zemlje, već Mesec i
Zemlja osciliraju oko jedne zajedničke tačke, oko zajedničkog centra mase
koji se zove baricentar. I zapravo tačka u kojoj se nalazi baricentar
obilazi Sunce po eliptičnoj putanji dok centri Meseca i Zemlje osciliraju
oko te tačke. Stoga ni putanja Meseca ni putanja Zemlje nemaju pravilan
eliptični oblik.
Međutim masa Zemlje je ipak dosta veca od mase Meseca te se baricentar nalazi mnogo bliže centru mase Zemlje od koga je udaljen 4700 kilometara dok je odaljenost od centra mase Mecesa nesto manje od 400 000 kilometara.
Baricentri i afine baze
Ako je A bilo koji afini prostor nad poljem K, ekemente skupa
![]() zovemo
i ponderisanim tačkama tog prostora A. Drugim rečima, to su svi
parovi (
zovemo
i ponderisanim tačkama tog prostora A. Drugim rečima, to su svi
parovi (![]() ),
gde je A neka tačka iz A i
),
gde je A neka tačka iz A i ![]() neki
skalar.
neki
skalar.
Za datu ponderisanu tačku (![]() )
odgovarajući skalar
)
odgovarajući skalar ![]() zovemo i koeficijentom ili masom, odnosno težinom same tačke A. Takođe,
ako je S neki system od n ponderisanih tačaka, tada suma
zovemo i koeficijentom ili masom, odnosno težinom same tačke A. Takođe,
ako je S neki system od n ponderisanih tačaka, tada suma
![]() njihovih
masa
njihovih
masa ![]() zovemo
masom samog tog sistema S. Pri tom:
zovemo
masom samog tog sistema S. Pri tom:
Tvrđenje 1. Za svakih n ponderisanih tačaka (![]() ),…,(
),…,(![]() ) u afinom prostoru A, čija ukupna masa
) u afinom prostoru A, čija ukupna masa ![]() nije 0, postoji tačno jedna tačka S za koju je
nije 0, postoji tačno jedna tačka S za koju je
(1) ![]() .
.
Dokaz. Ako je O fiksirana tačka iz A, biće ![]() pa odmah sledi da je relacija (1) ekvivalentna sa
pa odmah sledi da je relacija (1) ekvivalentna sa
![]()
![]() .
.
Štaviše, kako tu ![]() nije 0, time je ona ekvivalentna i sa
nije 0, time je ona ekvivalentna i sa
(2) ![]() .
.
Otuda i sama teorema , jer za datu tačku O i vektor ![]() na desnoj strain u (2) postoji tačno jedna tačka S za koju je
na desnoj strain u (2) postoji tačno jedna tačka S za koju je ![]() , a time i tačno jedna tačka S za koju važi (1).
, a time i tačno jedna tačka S za koju važi (1).
Tačku S o kojoj je reč u tvrđenju 1 zovemo i baricentrom uočenog sistema ponderisanih tačaka (![]() ),…,(
),…,(![]() ), ili samih tačaka
), ili samih tačaka ![]() sa masama
sa masama ![]() , za koje
, za koje ![]() nije nula. To je i jednina tačka prostora A, takva da za bar jednu, a time i svaku tačku O iz A važi (2).
nije nula. To je i jednina tačka prostora A, takva da za bar jednu, a time i svaku tačku O iz A važi (2).
Takođe, baricentar ponderisanih tačaka (![]() ,
,![]() ) se ne menja, ako se njihove mase pomnože istim skalarom
) se ne menja, ako se njihove mase pomnože istim skalarom ![]() . Naime, množeći (1) sa
. Naime, množeći (1) sa ![]() dobijena relacija tačno znači da je S baricentar ponderisanih tačaka (
dobijena relacija tačno znači da je S baricentar ponderisanih tačaka (![]() ,
,![]() ), sa istim tačkama
), sa istim tačkama ![]() i masama
i masama ![]() .
.
Štaviše, birajući tu ![]() tako da suma
tako da suma ![]() bude jedan, na taj način sledi i da je tačka S baricentar datih tačaka
bude jedan, na taj način sledi i da je tačka S baricentar datih tačaka![]() sa izvesnim masama, ako i samo ako postoje neki skalari
sa izvesnim masama, ako i samo ako postoje neki skalari ![]() , takvi da je
, takvi da je
(3) ![]()
![]()
za bar jednu, a tie i svaku tačku O. Naravno, tada je S baricentar i ponderisanih tačaka (![]() ,
,![]() ). U tom slučaju, umesto (3) takođe pišemo i
). U tom slučaju, umesto (3) takođe pišemo i
(4) ![]()
uz napomenu da ta relacija ima smisla jedino ako je i ![]() . Tako, na primer, sama relacija
. Tako, na primer, sama relacija ![]() znači da je tačka S baricentar datih tačaka A i B sa masama
znači da je tačka S baricentar datih tačaka A i B sa masama ![]() i
i ![]() . Prema prethodnom, to je ekvivalentno, kako sa
. Prema prethodnom, to je ekvivalentno, kako sa ![]() ,tako i sa
,tako i sa ![]() . To dalje znači i da je tačka S baricentar dve razne tačke A i B, sa izvesnim masama, ako i samo ako je i na pravoj
. To dalje znači i da je tačka S baricentar dve razne tačke A i B, sa izvesnim masama, ako i samo ako je i na pravoj ![]() . Takođe:
. Takođe:
Tvrđenje 2. Ako su E i F, tim redom, baricentri bilo koja dva sistema ponderisanih tačaka (![]() ),…,(
),…,(![]() ) i (
) i (![]() ),…,(
),…,(![]() ), takvih da nijedan od skalara
), takvih da nijedan od skalara
(5) ![]() ,
, ![]()
I ![]() nije nula, tada je baricentar S svih tih p+q tačaka upravo baricentar ponderisanih tačaka (E,
nije nula, tada je baricentar S svih tih p+q tačaka upravo baricentar ponderisanih tačaka (E, ![]() ) i (F,
) i (F, ![]() ). Pri tom su tačke E,F,S kolinearne i važi ES:SF=
). Pri tom su tačke E,F,S kolinearne i važi ES:SF=![]() .
.
Dokaz. Pre svega, ako je O bilo koja tačka prostora A, prema dokazu tvrđenja 1, tačke E i F su određene sa
![]() i
i ![]() .
.
Sada je iz istih razloga I
![]() ,
,
pa je tako tačka S baricentar i ponderisanih tačaka (E, ![]() ) i (F,
) i (F, ![]() ), sa ukupnom masom
), sa ukupnom masom ![]() . Otuda i samo tvrđenje, jer njegov preostali deo sledi direktno iz relacije
. Otuda i samo tvrđenje, jer njegov preostali deo sledi direktno iz relacije ![]() .
.
Jasno je da prethodno tvrđenje važi i za uniju tri ili više sistema ponderisanih tačaka. Njime se, za ![]() , određivanje baricentra datog sistema sa n tačaka može svesti na određivanje baricentara nekih sistema sa po manje od n tačaka.
, određivanje baricentra datog sistema sa n tačaka može svesti na određivanje baricentara nekih sistema sa po manje od n tačaka.
Posebno, ako postoji baricentar sistema tačaka ![]() , sa istim masama
, sa istim masama ![]() , zovemo i njegovim težištem. Naravno, tu mora biti i
, zovemo i njegovim težištem. Naravno, tu mora biti i ![]() što sigurno važi ako je polje K karakteristike 0, na primer za K=R. Drugim rečima, to je jedina tačka T prostora A za koju je
što sigurno važi ako je polje K karakteristike 0, na primer za K=R. Drugim rečima, to je jedina tačka T prostora A za koju je ![]() , a time i
, a time i
![]()
za svaku tačku O iz A. Takođe, ako je tačka ![]() različita od težišta
različita od težišta ![]() preostalih tačaka iz S, tako određene prave
preostalih tačaka iz S, tako određene prave ![]() zovemo i težišnim pravama uočenog sistema tačaka S. Prema prethodnom tvrđenju 2, za p=1, sve one sadrže njegovo težište T i pri tom važi
zovemo i težišnim pravama uočenog sistema tačaka S. Prema prethodnom tvrđenju 2, za p=1, sve one sadrže njegovo težište T i pri tom važi
![]()
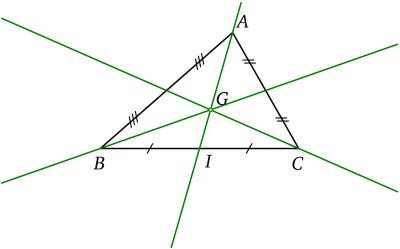
Slika 2. Trougao i njegov baricentar (težište)
Tako, na primer, ako polje nije karakteristike 2, jedina težišna prava dve različite tačke A i B je upravo ![]() , dok je njihovo težište
, dok je njihovo težište ![]() određeno sa
određeno sa ![]() , odnosno
, odnosno ![]() Takođe, ako polje K nije karakteristike 2 ili 3 sistem S nekolinearnih tačaka A,B,C ima tri težišne prave
Takođe, ako polje K nije karakteristike 2 ili 3 sistem S nekolinearnih tačaka A,B,C ima tri težišne prave ![]() ,
, ![]() i
i ![]() . One sadrže njegovo težište
. One sadrže njegovo težište ![]() i pri tom je
i pri tom je
![]() ,
,
![]() , i ako dalje. i slično za sistem tačaka
, i ako dalje. i slično za sistem tačaka ![]() , među kojima nikoje tri nisu kolinearne. Na osnovu tvrđenja 1 sledi da se, u opštem slučaju, njegovo težište T nalazi na sedam naznačenih pravih. Jedna od njih je i težišna prava
, među kojima nikoje tri nisu kolinearne. Na osnovu tvrđenja 1 sledi da se, u opštem slučaju, njegovo težište T nalazi na sedam naznačenih pravih. Jedna od njih je i težišna prava ![]() . Pri tom je
. Pri tom je ![]() ,
, ![]() , i tako dalje.
, i tako dalje.
Najzad, ako su ![]() i
i ![]() sistemi koordinata dve različite tačke A i B u odnosu na dati reper
sistemi koordinata dve različite tačke A i B u odnosu na dati reper ![]() prostora A dimenzije n i
prostora A dimenzije n i ![]() , prema (2), ada su i koordinate baricentra S ponderisanih tačaka (
, prema (2), ada su i koordinate baricentra S ponderisanih tačaka (![]() ) i (
) i (![]() ) određene sa
) određene sa
![]() .
.
Pri tom, ako je tu, na primer, ![]() i
i ![]() , te relacije se svode na
, te relacije se svode na
![]() .
.
ime su to i koordinate tačke S prave ![]() za koju je
za koju je ![]() , to jest,
, to jest, ![]() . Za
. Za ![]() , ta tačka S je upravo težište tačaka A i B, koje takođe zovemo i središtem para tačaka
, ta tačka S je upravo težište tačaka A i B, koje takođe zovemo i središtem para tačaka ![]() .
.
Literatura:
- Gojko Kalajdžić, Mirjana Đorić, Osnovi Geometrije
- Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers. (2004).
- Astronomski magazin- www.astronomija.co.yu
preuzmi
seminarski rad u wordu » » »


