OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
ENERGIJA
 Energija
je sposobnost tela ili sastava tela da obavljaju rad: što telo
ima veću energiju, to je sposobnije da obavi veći rad.
Energija
je sposobnost tela ili sastava tela da obavljaju rad: što telo
ima veću energiju, to je sposobnije da obavi veći rad.Kad telo obavlja rad, energija mu se smanjuje, i obratno, ako okolina obavlja rad na telu, energija tela se povećava. Rad može prelaziti u energiju i obratno. Jedinica rada i energije je identična.
Postoji više oblika energije: mehanička, električna, termalna (unutrašnja), hemijska, solarna, nuklearna... Uopsteno, postoje mehanički i nemehanički oblici energije.
Mehanička energija makroskopskih tela ili sastava tela je zbroj kinetičke i potencijalne energije tih tela.
Kinetičku energiju uzrokuje gibanje tela nekom brzinom, a potencijalnu energiju uzrokuje položaj tela unutar sastava. Potencijalna i kinetička energija mogu se pretvarati jedna u drugu, mehanička energija može prelaziti u nemehaničke oblike energije i obratno. Energija može prelaziti iz jednog oblika u drugi, ali se ne može ni stvoriti ni uništiti.
U svakodnevnom zivotu rec ”rad” se primenjuje za aktivnosti ko je zahtevaju bilo kakav oblik fizickog ili umnog naprezanja. U fizici je upotreba ovog termina ogranicena. Naime, poznato je da tela medjusobno mogu delovati razlicitim silama (sile trenja, gravitacije, elasticne sile, elektromagnetne sile, itd.), sto dovodi do njihovog pomeranja. Za karakterisanje ovih pojava koristi se velicina koja je utoliko veca ukoliko je veca komponenta sile duz pravca pomeranja i ukoliko se na vecu daljinu premesta njena napadna tacka. Ta velicina u fizici je poznata pod nazivom rad.
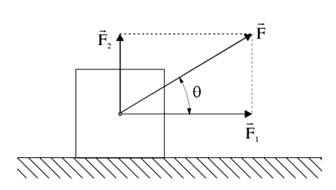
Najjednostavniji slucaj vrsenja rada je kada na telo deluje konstantna sila
![]()
Ako je sila ![]() konstantna i deluje pod uglom u odnosu na pravolinijsko pomeranje
tela izvrseni rad jednak je proizvodu komponente sile paralelne pomeranju
i samog pomeranja, tj.
konstantna i deluje pod uglom u odnosu na pravolinijsko pomeranje
tela izvrseni rad jednak je proizvodu komponente sile paralelne pomeranju
i samog pomeranja, tj.
![]()
Ako je θ< 90˚, tj. ako sila i put zaklapaju ostar ugao, rad je pozitivan (A > 0), za θ> 90˚ je negativan (A < 0), a ako je θ = 90, ne vrsi se rad (A = 0).
Izrazi i predstavljaju specijalne sluca jeve vrsenja rada. Naj opstiji
sluca j je kada se sila koja deluje na telo menja i po pravcu i po intenzitetu,
a kretanje vrsi po krivolinijskoj putanji. Da bi se odredio rad ovakve
sile na putu od s1 do s2, potrebno je put izdeliti na elemente ds, na
kojima se moze smatrati da je sila konstantna, a pomeranje pravolinijsko.
Tada elementarni rad iznosi
![]()
a ukupan rad na putu o d s1 do s2 odredjen je integralom
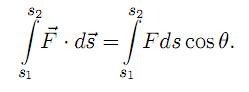
Za izracunavanje ovog integrala neophodno je poznavati zavisnost F od s duz trajektorije s1 s2.
Ako je ta zavisnost oblika trazeni rad A odredjen je zasencenom povrsinom na grafiku
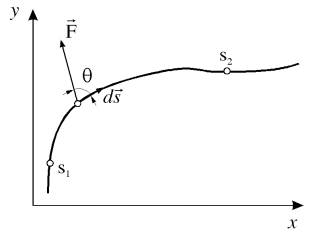
Sl. Uz objasnjenje rada promenljive sile
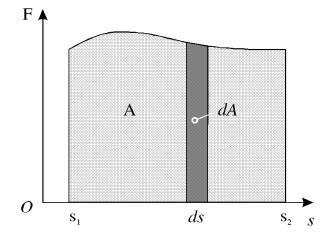
Sl. Graficki prikaz rada promenljive sile
Ako se telo krece pravolinijski i ako je F = const: i
= const:, onda je
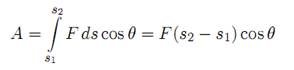
ili
![]()
gde je s2 – S1 = S put ko ji telo predje pod dejstvom promenljive sile. Jedinica za rad je Dzul (J ).
Snaga
U praksi je cesto potrebno, pored poznavanja rada koji izvrsi neka sila, poznavati i vreme za koje je taj rad izvrsen. Naime, u tehnickom pogledu sila je utoliko korisnija ukoliko za krace vreme izvrsi neki rad. Za karakterisanje brzine vrsenja rada koristi se fizicka velicina koja se naziva snaga ili efekat. Snaga je jednaka odnosu rada ∆A i vremenskog intervala za koji se taj rad izvrsi ∆t:
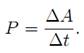
Ovaj izraz vazi za slucaj kada je odnos ∆A = ∆t stalan, odnosno kada je snaga konstantna velicina. Kada se snaga menja sa vremenom, izraz da je srednju vrednost snage u intervalu ∆t .
Za slucaj promenljive snage (za jednake vremenske intervale vrsi se razliciti rad) uvodi se pojam trenutne snage.
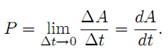
Snaga se moze izraziti preko sile i brzine na sledeci nacin:

Jedinica za snagu je Vat (W ). Jedan W predstavlja rad od 1J u 1s ( W = J /s).
Jedinica za rad se moze izraziti preko jedinice za snagu kao J = W * s.
Zato se u tehnici J cesto naziva vatsekund (Ws). U upotrebi je veca jedinica za rad —kilovatcas (kWh), kojom se meri potrosnja elektricne energije.
Energija
Svi oblici kretanja materije pri odredjenim uslovima mogu prelaziti jedan u drugi u strogo odredjenim kvantitativnim odnosima. Ova pojava je omogucila merenje razlicitih oblika kretanja istom merom, sto je uslovilo uvodjenje pojma energije. Energija je opsta mera za razlicite procese i oblike medjusobnog dejstva.
Promena energije tela ili sistema tela ∆E proporcionalna je radu A koji vrse spoljasnje sile kada deluju na telo (sistem), tj.
![]()
gde je K koeficijent proporcionalnosti. Ako se uzme da je K = 1, onda je
![]()
Ova jednakost se naziva teorema o radu i energiji.
Kada je rad spoljasnjih sila pozitivan (sila vrsi rad), energija raste, i obrnuto, kada je ovaj rad negativan (telo vrsi rad), energija sistema se smanjuje. Prema tome, telo moze da vrsi rad samo na racun promene svoje energije. Ako je rad ko ji vrsi neki sistem tela jednak nuli, onda je to zatvoren sistem.
Na osnovu prethodno iznetog moze se zakljuciti da je energija velicina
ko ja karakterise stanje nekoga tela, a rad velicina koja karakterise
promenu tog stanja. Telo (sistem)
poseduje energiju, a rad predstavlja proces prenosenja energije sa jednog
tela na drugo, ili proces pretvaranja jednog oblika energije u drugi.
Na primer, kada kuglica ko ja se krece o dredjenom brzinom udari u nepokretnu
kuglicu, predaje joj deo svo je energije, usled cega i ona p ocinje da
se krece.
Postoji vise oblika energije, kao sto su mehanicka, toplotna, elektricna,
hemijska, nuklearna, itd.
Kinetička energija
Kineticka energija tela (materijalne tacke) predstavlja meru njegovog mehanickog kretanja i odredjuje rad koji je neophodno izvrsiti da bi doslo do kretanja tela.
Neka je u momentu p osmatranja telo imalo brzinu v
Delovanjem sile F njegova brzina se povecala i iznosi
v21, a energija se povecala za vrednost utrosenog rada. Rad sile F
na putu od s, gde je brzina v1, do s2, gde je brzina v2, iznosi

Posto je F = mdv / dt, to je
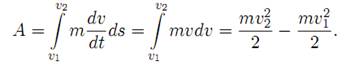
Ako se uporedi ovaj izraz sa teoremom ![]() moze se zapaziti da
moze se zapaziti da ![]() predstavlja
kineticku energiju tela kada se krece brzinom
predstavlja
kineticku energiju tela kada se krece brzinom ![]() njegovu kineticku energiju kada se krece brzinom v2. Stoga se, u opstem
slucaju, kineticka energija moze matematicki izraziti kao
njegovu kineticku energiju kada se krece brzinom v2. Stoga se, u opstem
slucaju, kineticka energija moze matematicki izraziti kao

Ako se radi o sistemu tela (materijalnih tacaka), cije su mase m1, m2,
m3,. . . ,mn, a brzine v1, v, v3,. . . , vn, ukupna kineticka energija
sistema je
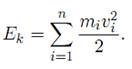
Iz izraza ![]() se vidi da kineticka energija zavisi samo od mase i brzine tela, dakle,
ona je funkcija stanja njegovog kretanja.
se vidi da kineticka energija zavisi samo od mase i brzine tela, dakle,
ona je funkcija stanja njegovog kretanja.
Pri izvodjenju izraza ![]() pretpostavljeno je da se kretanje razmatra u inercijalnom sistemu referencije,
jer se u protivnom ne bi mogao koristiti Njutnov zakon.
pretpostavljeno je da se kretanje razmatra u inercijalnom sistemu referencije,
jer se u protivnom ne bi mogao koristiti Njutnov zakon.
U razlicitim inercijalnim sistemima referencije, koji se krecu jedan u
odnosu na dugi,brzina tela, a time i njegova kineticka energija, bice
razlicita.
Prema tome, kineticka energija zavisi od izbora sistema referencije.
Potencijalna energija
Telo poseduje energiju ne samo pri kretanju, vec i kada se nalazi u odredjenom
polozaju u prostoru. Takva energija naziva se potencijalna energija.
Uobicajen primer potencijalne energije jeste gravitaciona potencijalna
energija. Telo odredjene mase podignuto na neku visinu ima gravitacionu
potencijalnu energiju zahvaljujuci svom polozaju, jer ima mogucnost da
izvrsi rad prilikom pada sa te visine. Primer za ovo je pobijanje stapa
u zemlju pod udarom cekica. Podizanje tela mase m vertikalno navise moguce
je samo ako se na njega deluje silom koja je barem jednaka sili teze mg
(ovo vazi za male visine, kada je g = const:). Da bi se telo podiglo na
visinu h od p ovrsine zemlje, mora se izvrsiti rad mgh. Ako se pusti da
telo pada sa te visine, ono ce izvrsiti rad mgh .
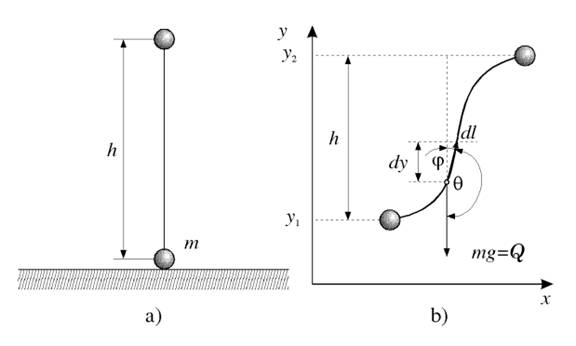
Neka se, umesto kretanja navise po vertikali,
telo krece po nekoj proizvoljnoj putanji u ravni xy. Ono pocinje sa kretanjem
u tacki sa ordinatom (visinom) y1i dostize visinu y,
pri cemu je y2 - y1= h . Rad ko ji izvrsi sila pri pomeranju za dl je
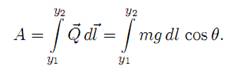
Sa slike b se vidi da je θ = 180 – φ’ , pa je cos θ = - cos φ, a dl = dy / cos φ, tako da izraz dobija oblik

gde je y= h visina izmedju dva izabrana polozaja tela. Iz
izraza vidi se da rad sile zavisi od visine, ali ne i od oblika trajektorije.
Takve sile nazivaju se konzervativne sile.
Za slucaj prikazan na slici b je y2 > y1, pa je rad
sile teze negativan. Ako je y (telo pada nanize), rad je pozitivan. Ako
telo pada slobodno sa visine h = y2 - y1, ono nad drugim telom ili sistemom
moze izvrsiti rad jednak mgh = mg (y). Na osnovu teoreme moze se odrediti
promena potencijalne energije ∆ Ep , kada se telo pomeri iz tacke sa koordinatom
y1u tacku sa koordinatom y2
![]()
Prema tome, gornji izraz odredjuje promenu potencijalne energije izmedju
dve tacke.
U saglasnosti sa izrazima, kao i teoremom potencijalna energija u datoj
tacki, na visini h u odnosu na referentni nivo, data je izrazom.
![]()
Uporedjivanjem izraza moze se zapaziti da je promena potencijalne energije jednaka radu koji vrsi sila teze pri premestanju tela sa visine y1na visinu y2, sa znakom minus, tj.

Umesto ovog treba reci da je promena potencijalne energije ∆Ep jednaka
radu koji vrsi neka druga sila, jednaka po intenzitetu sili teze, koja
potice od coveka koji (bez trenja) pomera telo suprotno sili teze.
U sabijenom ili rastegnutom stanju opruga prikazana na slici oseduje potencijalnu
energiju koja, kada se oslobodi, moze da izvrsi rad nad kuglicom. Neka
je koordinatni sistem izabran tako da se kraj rastegnute opruge nalazi
u tacki x = 0, a pozitivni pravac je desni deo x-ose. Da bi se opruga
odrzala u sabijenom (ili rastegnutom) stanju na rastojanju x, potrebno
je na nju delovati silom F = k x. Po Trecem
Njutnovom zakonu opruga deluje na kuglicu silom Fs , istog intenziteta,
a suprotnog smera Fs = - kx
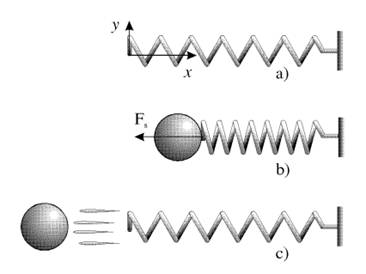
Opruga moze akumulirati elasticnu potencijalnu energiju kada je istegnuta (a) ili sabijena (b);
ova energija se moze iskoristiti za vrsenje rada u trenutku njenog oslobadjanja (c)
U gornjem izrazu znak (–) pokazuje da su smerovi sila F i Fs suprotni (slika b). Promena potencijalne energije opruge izmedju koordinata x1 = 0 (kada opruga nije deformisana) i x2 = x je

gde je Ep (x) potencijalna energija na rastojanju x, a Ep (0) potencijalna energija u tacki
x = 0. Prema tome, potencijalna energija opruge na rastojanju x od ravnoteznog polozaja data je izrazom

Ova energija poznata je pod nazivom elasticna potencijalna energija.
Zakon održanja energije
Zakon o drzanja energije proizasao je na osnovu
niza eksperimenata. Da bi se doslo do zakona odrzanja mehanicke energije,
posmatrace se sistem tela (materijalnih tacaka),cije su mase m1, m2, m3,.
. . ,m i brzine v1, v2, v3,. . . ,vn. Neka na ova tela deluju unutrasnje
sile F1, F2, F3,. . . , Fnn i spoljasnje sile F, Fs 2, Fs3,. . . , Fsn.
Iz Drugog Njutnovog zakona sledi

Neka se tela za isti vremenski interval dt pomere za rastojanja dx1, dx2,
dx3,. . . ,dx. Mnozenjem svake od jednacina u odgovarajucim pomerajem
i uzimajuci da je dxi = vi dt, dobija se
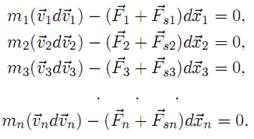
Sabiranjem ovih jednacina, uzimajuci da je sistem zatvoren, tj.
![]()
dobija se

Clan

predstavlja beskonacno malu promenu kineticke, a ![]() beskonacno malu promenu potencijalne energije celog sistema. Prema tome,
izraz se moze napisati u obliku
beskonacno malu promenu potencijalne energije celog sistema. Prema tome,
izraz se moze napisati u obliku
![]()
Ukupna mehanicka energija zatvorenog sistema je
![]()
Ovaj izraz predstavlja Zakon odrzanja mehanicke energije. On glasi:
U zatvorenom sistemu tela izmedju kojih deluju samo konzervativne sile
mehanicka energija se odrzava, tj. ne menja se u toku vremena.
Vezano za zakon odrzanja mehanicke energije, postoji teorema o minimumu
potencijalne energije, ko ja glasi:
Stabilno stanje zatvorenog sistema je ono kod kojeg je potencijalna energija
sistema minimalna.
Ukupna mehanicka energija sistema u kome deluje sila trenja smanjuje se
pri kretanju. U tom slucaju ne vazi Zakon o drzanja mehanicke energije.
Medjutim, pri ”iscezavanju” mehanicke energije uvek postoji
ekvivalentna kolicina energije drugog oblika. Prema tome:
Energija ne iscezava i ne pojavljuje se nova, vec samo prelazi iz jednog
oblika u drugi.
U tome sto govori o neunistivosti materije i njenog kretanja i jeste fizicka
sustina Zakona o drzanja energije.
Postoji niz primera koji ilustruju Zakon odrzanja mehanicke energije.
Jedan od najjednostavnijih, jeste slobodno padanje tela bez pocetne brzine
u uslovima kada se sila trenja sa vazduhom moze zanemariti.
Neka se telo mase (m) nalazi na visini (h) iznad Zemlje. Posto telo na
ovoj visini miruje, raspolaze samo potencijalnom energijom, tj. njegova
ukupna energija E jednaka je potencijalnoj energiji mgh.
Kada se pusti da telo pada, njemu se tokom kretanja smanjuje potencijalna
na racun povecanja kineticke energije. Medjutim, ukupna energija u bilo
kojoj tacki putanje ostaje ista.

Primer zakona odrzanja mehanicke energije.
Na primer, u tacki B na visini h1, gde je brzina v, kineticka i potencijalna
energija tela su
![]()
U tom slucaju ukupna energija je
![]()
Na osnovu izraza brzina se moze izraziti kao
![]()
Zamenom izraza, za ukupnu energiju se dobija
![]()
sto je jednako energiji koju je telo imalo na visini h. Neposredno pre
udara o zemlju (tacka C ), kineticka energija tela je
![]()
gde je v1njegova brzina neposredno pre udara. Potencijalna energija u
ovom slucaju je Ep= 0.
LITERATURA:
- Momcilo M. Pejovic – Opsta fizika
- www.wikipedia.org
preuzmi
seminarski rad u wordu » » »


