OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
OPTIČKA SOČIVA
Optička sočiva su optička tela, izrađena od providnih materijala(staklo, kvarc) koja su ograničena dvema sfernim površinama ili jednom sfernom i jednom ravnom površinom.
Za svako sočivo defninisaćemo njegove elemente:
- Centri krivine, C1 i C2 koji zapravo predstavlaju i centre sfera u čijem se preseku nalazi sočivo
- Glavna optička osa, prava koja spaja C1 i C2
- Optički centar-O- je tačka kroz koju mogu da prođu zraci a da se ne prelamaju. Nalazi se u preseku glavne optičke ose sa pravom koja deli sočivo na dva jednaka dela.
- Žiža(fokus) je tačka u kojoj se seku prelomljeni zraci.
Sočiva možemo da podelimo na osnovu različitih kriterijuma.
Prema debljini:
- Tanka
- Debela
Prema načinu prelamanja svetlosti:
- Sabirna
- Rasipna
Tanko sočivo je ono sočivo čija je debljina mnogo manja u odnosu na poluprečnike krivina sfera u čijem je preseku nastalo.
Sabirna sočiva su ona sočiva kod kojih prelomljeni zraci seku glavnu optičku osu
Rasipna sočiva su ona sočiva kod kojih prelomljeni zraci divergiraju, tj udaljavaju se od glavne optičke ose.
Sabirna sočiva se dele na:
- Bikonveksna
- Plankonveksna
- Konkavnokonveksna
Rasipna sočiva se dele na :
- Bikonkavna
- Plankonkavna
- Konveksno konkavna
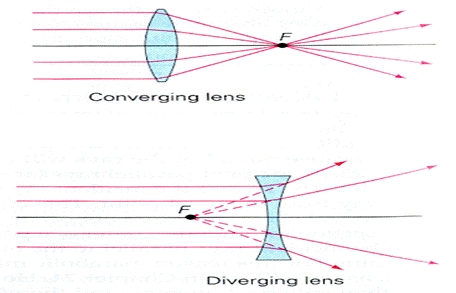
FORMIRANJE ŽIŽE KOD SABIRNOG SOČIVA:
Kod sabirnog sočiva svi prelomljeni zraci prolaze kroz jednu tačku i ta tačka je ZADNJA ŽIŽA. Kod sabirnog sočiva žiža je realna.
FORMIRANJE ŽIŽE KOD RASIPNOG SOČIVA:
Svetlosni zraci kod rasipnog sočiva divergiraju i produžeci tih zraka seku se u prednjoj žiži. Žiže rasipnih sočiva su imaginarne. Rasipnim sočivom se ne može dobiti realan lik predmeta pa se za određivanje žižne daljine najčešće pravi kombinacija rasipnog sočiva i sabirnog sočiva.
OPTIČKA MOĆ SOČIVA:
Za svako sočivo se definiše optička moć sočiva J,i predstavlja meru veličine prelamanja svetlosti ili meru konvergencije. Recipročna je vrednost žižne daljine, pa se može pisati:
J=ns/f
ns –indeks prelamanja za date sredine koje okružuju sočivo. Ako se nalazi u vazduhu ns je 1 pa je optička moć:
J=1/f, jedinica je 1D=1m-1
Sočivo ima optičku moć od 1D ako je njegova žižna daljina 1m
TANKO SOČIVO I JEDNAČINA TANKOG SOČIVA:
Jednačina tankog sočiva koja daje zavisnost daljine lika i daljine predmeta od poluprečnika krivina, može se izvesti na osnovu Fermatovog principa, koji za posmatrani slučaj glasi:
Pri odbijanju ili prelamanju svetlosti od ravne ili sferne površine, svetlost prođe onaj put za koji je potrebno najkraće vreme
Aproksimativna j-na tankog sočiva: (n-1)(1/R1 + 1/R2)=1/p +1/l
Ako je svetli predmet u beskonačnosti,lik predmeta biće u zadnjoj žiži
sočiva na rastojanju l=f. Tada će j-na biti: (n-1)(1/R1 + 1/R2)=1/f=1/l
Tj
1/p + 1/l=1/f
KARAKTERISTIČNI ZRACI:
Za konstrukciju likova predmeta konačnih dimenzija koristimo grafičke metode, tj imamo 3 karakteristična zraka pomoću kojih konstruisemo lik predmeta. To su:
- Zrak svetlosti koji pada na sočivo paralelno sa glavnom optičkom osom, i prelama se tako da prolazi kroz žižu sa druge strane sočiva
- Zrak svetlosti koji pada u optički centar sočiva i prolazi bez prelamanja
- Zrak svetlosti koji prolazi kroz žižu sočiva, prelama se tako da je paralelan optičkoj osi.


UVEĆANJE SOČIVA:
Linearno uvećanje sočiva jeste linearan odnos linearnih dimenzija lika i predmeta
U=L/P=l/p
tj uvećanje sočiva je jednako odnosu daljine lika i daljine predmeta
Da li će lik biti umanjen ili uvećan, uspravan ili izvrnut, relana ili imaginaran, zavisi od rastojanja predmeta od sočiva.
KOMBINOVANO SOČIVO:
Kombinovano sočivo dobijamo kada dva ili više tankih sočiva postavimo
tako da njihovi centri krivina leže na glavnoj optičkoj osi. Takav sistem
sočiva se naziva centrirani.
Prelamanje svetlosti se vrši tako da svetlosni zrak
pada na prvo sočivo, prelama se, i tako prelomljeno predstavlja upadni
zrak za drugo sočivo, i tako redom do zadnjeg sočiva. Lik koji daje svako
prethodno sočivo služi kao predmet svakom narednom sočivu. 
![]() žiža
kombinovanog sočiva
žiža
kombinovanog sočiva
LUPA
Lupa je optički instrument koji uvećava sitne predmete, tako da ih jasnije
vidimo. To je zapravo sabirno sočivo jako male žižne daljine.
1/p - 1/d = 1/f, d-daljina jasnog vida
U=d/f+1 – uvećanje lupe
MIKROSKOP
Da bi smo videli jako sitne predmete koji se ne mogu videti golim oko
koristimo MIKROSKOP. On se sastoji od dva centrično postavljena sistema
sabirnih sočiva malih žižnih daljina. Jedan sistem sočiva upotrebljava
se kao objektiv, koji od sićušnog predmeta daje realan
i uvećan lik. Taj lik je predmet za drugi sistem sočiva, okular,
okrenut oku.Ukupno uvećanje mikroskopa jednako
je prozvodu uvećanja objektiva i uvećanja okulara:
U=s*d/f1*f2 uvećanje mikroskopa
DISPERZIJA SVETLOSTI
Pojava disperzije predstavlja zavisnost indeksa prelamanja sredine od talasne dužine .
Praktično pod disperzijom se podrazumeva pojava razlaganja bele svetlosti u spektralne boje različitih talasnih dužina.
Međutim prema klasičnoj Lorencovoj teoriji disperzija svetlosti se posmatra kao uzajamno dejstvo elektromagnetnih talasa i naelektrisanja čestica sredine kroz koje talas prolazi.
Zavisnost indeksa prelamanja od talasne dužine je dat Košijevom relacijom:
n=A + B/λ2 + C/λ4
U formuli A, B, C jesu konstante koje zavise od prirode sredine.
Osobine nekog spektra izražavaju e pomoću dve veličine:
- Mera ili veličina disperzije Dδ
- Moć disperzije ω
Veličina disperzije određuje se razlikom ugla skretanja monohromatkse svetlosti talasnih dužina λ1 λ2 koje odgovaraju crvenoj i tamnoplavoj svetlosti koju daju atomi vodonika u odnosu na srednju liniju žute natrijumove svetlosti
Disperziona moć je odnos mere disperzije i ugla skretanja srednjeg zraka
ω= Dδ/δD
Kakav će biti disperzioni spektar zavisi od karaktera svetlosnog izvora. Postoje tri osnovna obilka spektra:
- Kontinualni
- Linijski
- Trakasti
Kontinualni spektri se javljaju kod usijanih
tela koja zrače svetlost. Kod takvih spektara nema oštre granice između
spektralnih boja. U spektru Sunca npr vidimo Fraunhoferove linije
Linijski spektri se zapažaju kod usijanih para
i gasova koji su pod određenim pritisom.
Trakasti spektri se javlaju kod moelkulskih spektra
para i gasova, pri čemu su spektralne linije u vidu traka, te otuda im
i takav naziv.
APSORBCIJA SVETLOSTI
Često puta smo primetli da se pri prostiranju svetlosti kroz neku sredinu njen intezitet(energija) smanjuje. Ta pojava zove se apsorbcija svetlosti.
Jedan deo svetlosti koja se apsorbovala troši se na pobuđivanje atoma apsorbujuće sredine
Zakon apsorbcije
Intezitet svetlosti ravnog talasa monohromatske svetlosti,pri prolazu kroz apsorbcionu sredinu dužine x,menja po eksponencijalnom zakonu:
I=Ioe-αx
Io intezitet svetlosti na ulazu u apsorbujući sloj
I-intezitet izlazne svetlosti α-koeficijent apsorbcije sredine
RASEJANJE SVETLOSTI
Rasejanje ili rasprašavanje svetlosti se javlja u optički nehomogenim sredninama,čija je homogenost narušena prisustvom sićušnih čestica(dim,magla,koloidni rastvori..) Sekundarni talasi se uzajamno ne poništavaju, već na tim centrima nehomogenosti difraktuju u vidu ravnomernog osvetljenja u svim pravcima izazivajući pojavu rasejanja
INTERFERENCIJA SVETLOSTI
Pri prostiranju talasa sem odbijanja i prelamanja može doći i do interferencije talasa. Interferencija talasa je pojava da na pojednim mestima delići elastične sredine osciluju sa maksimalnim amplitudama(max intereferencije), a na drugim mestima oscilacije su minimalne.
Mesta maksimuma i minuma su uslovljena putnom razlikom između tih talasa,tj njihov faznom razlikom.
U onim tačkama sredine gde je putna razlika jednaka celobrojnom umožku talasne dužine se javlja maksimum interferencije Dr=mλ ,a u tačkama gde je ta putna razlika jednaka neparnom broju polovina talasne dužine dobijaju se minimumi interferencije Dr=(2m+1)λ/2
Da bi moglo da dođe do interferencije talasi moraju da budu koherentni tj da imaju istu frekvenciju i period oscilovanja.
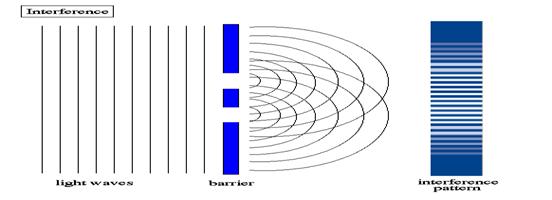
Metode Za Posmatranje Iterferencije Svetlosti
Prvu interferenciju svetlosti je izvršio Jung, tako što je pustio da snop monohromatkse svetlosti pada na zaklon Z koji ima dva mala otvora. Ti otvori postaju izvori koherentnih svetlosnih talasa koji se u vidu polusfera prostiru u svim pravcima.
Do konstruktivne interefernecije će doći ako ako talasi dopseju sa putnom razlikom : Dr = r2-r1 =mλ
Do destruktivne intereferencije će doći u onim tačkama prostora gde je putna razlika: Dr=(2m+1)λ/2
Druga metoda za dobijanje koherentne svetlosti jeste zapravo primena Frenelovih ogledala koji je izveo ogled interferencije sa dva ravna ogledala postavljena pod uglom nešto manjim od 180 stepeni.
Izvor monohromatkse svetlosti je postavljen tako da svetlosni zraci padaju na ogledala padaju pod različitim uglom. Produžeci odbijenih zraka seku se iza ogledala stvarajući dva imaginarna svetla lika. Svetlosni zraci imaginarnih likova daju koherentnu sliku.
Interferencija svetlosti je danas našla primenu kod raznih fizičkih eksperimenata u cilju otklanjanja neželjenih refleksija,raznih aberacija idr.
DIFRAKCIJA SVETLOSTI
Do pojave difrakcije dolazi ako svetlost na svom putu pada na male(uske) otvore ili oštre prepreke čije su dimenzije reda veličine talasne dužine svetlosti,pa svetlost odstupa od svog pravolinijskog prostiranja tj dolazi do savijanja(difrakcije) svetlosnih talasa.
Hajgens-Frenelov Pricip
Po Hajgensu svaka tačka difrakcionog otvora ili prepreke pogođena talasom i sama postaje izvor novih elementarnih talasa.
Frenel je taj princip matematički uobličio. Dakle po tom principu proističe da difrakcija talasa nije ništa drugo no interferencija mnoštvo koherentnih talasa koji potiču od svih tačaka geometrijskog otvora ili rubova prepreke.
Slaganje svih tih talasa dovodi do uzajamnog pojačavanja ili slabljena inteziteta svetlosti,što u ravni njihovog ukrštanja uslovljava izražene efekte difrakcije u vidu naizmenično svetlih i tamnih mesta.
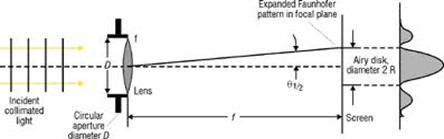
Fraunhoferova Difrakcija Na Uskom Prorezu
Fraunhoferov tip difrakcije svetlosti ima veći praktični značaj od Frenelovog
tipa.Da bi efekti bili vidljivi, izvor svetlosti se postavlja u žiži jednog
sabirnog sočiva,a difrakciona slika se posmatra u žižnoj ravni drugog
sočiva.
Efekti difrakcije svetlosti na uskom prorezu,dobijani eksperminetlanim
putem ,pokazuju da se difrakciona slika sastoji od jednog širokog centalnog
maksimuma,a sa obe njegove strane se nalaze naizmenično tamni i svetli
pojasevi
Difrakcija Svetlosti Na Optičkoj Rešetki
Ukoluko želimo da ostavrimo bolje efekte difrakcije svetlosti koristićemo
jednodimenzionalnu optičku rešetku. Optička rešetka se pravi tako što
se na staklenoj ploči vrhom dijamantske igle zapara veliki broj paralelnih
linija na jednakom rastojanju tako da upadna svetlost može prolaziti samo
na mestima između tih zareza. Takva difrakciona rešetka je transmisiona.
Rešetka kod koje se zarezi nanose na poliranoj metalnoj ili ogledalnoj
površini se naziva refleksiona
POLARIZACIJA SVETLOSTI
Prirodna svetlost sa bilo kog izvora je nepolarizovana. Kod takve svetlosti nema istaknutog pravca oscilovanja vektora polja nad drugim pravcima. Međutim eksperimentalno je dokazano da se pod izvesnim uslovima svetlosne oscilacije vektora polja ne vrše podjednako u svim pravcima, koji su normalni na pravac prostiranja talasa, već su, pri tome, pojedini pravci naročito istaknuti. Za takvu svetlost kaže se da je polarizovana.
Pojavu polarizacije svetlosti Jung i Frenel su objasnili kao proces uzajamnog delovanja prirodne svetlosti sa materijalnom sredinom, pri čemu se pod izvesnim uslovima , prirodna nepolarizovana svetlost pretvara u poalrizovanu.
Dobijanje Linerano Polarizovane Svetlosti
Nepolarizovana svetlost se može pretvoriti u polarizovanu pomoću uređaja koji se nazivaju polarizatori.
- U svojstvu polariztora koristimo kristal turmalina kao anizotropno sredstvo.
Na ploču P, izrezanu iz kristala turmalina pada normalno nepolarizovan zrak. Izlazna svetlost biće linearno polarizovana,i njene oscilacije biće paralelne optičkoj osi polarizatora. Ako na pultu izlaznog zraka postavimo kos jednu turmalinsku ploču A njenim okretanjem oko zaka kao ose, zapaža se izvesna promena izlaznog inteziteta svetlosti. Ta ploča A kojom se vrši analiza izlazne svetlosti naziva se analizator.
Ako optičke ose analizatora i polarizatora zaklapaju ugao Q tada će intezitet
te svetlosti biti:
I=I0cos2Q -Malusov zakon
I0 intezitet izlaznog zraka iz ploče P, I-intezitet izlaznog zraka iz
ploče A
Polarizacija svetlosti pri odbijanju i prelamanju
Ako nepolarizovana svetlost pada pod uglom α na graničnu površinu indeksa
prelamanja 1 jedan deo te svetlosti se odbija po zakonu odbijanjama drugi
deo se prelama kroz drugu sredinu po zakonu prelamanja.
Ako se na putu prelomljenog i odbijenog zraka postavi analizator, on pokazuje
da oba zraka jesu delimično polarizovana.
Škotski fizičar Bruster je ustanovio zakon po kome se
postiže maksimalna linearna polarizacija u odbijenom i prelomljenom zraku.
Po tom zakonu, odbijena svetlost biće potpuno polarizovana (100%),a propuštena
maksimalno, ali ne i potpuno,ako ona dolazi pod upadnim uglom αB za koji
odbijeni i prelomljeni zrak obrazuju pravi ugao
tgαB =n -Brusterov zakon
Polarizacija svetlosti dvojnim prelamanjem
Svi prozračni kristali pokazuju osobinu dvojnog prelamanja svetlosti
tj više razdvajanje upadnog zraka na dva zraka. Ovu pojavu je otkrio Bartolino.
Ako se na deblji kristal usmeri uski snop prirodne svetlosti pod kosim
uglom iz kristala izlaze dva prostorno razdvojena zraka koji su paralelni
jedan drugome, i uz to paralelni sa upadnim zrakom.
Za slučaj kada je upadna svetlost normalna na površinu kristala jedan
od tih zraka produži bez prelamanja i taj zrak je redovan zrak(r),a
drugi skreće i naziva se neredovan zrak(n).
Ako se iza kristala postavi analizator tada bi projekcija svetlog kružića
redovnog zraka na ekranu bila nepokretna,a svetli kružić neredovnog zraka
bi se okretao oko svetlog kružića redovnog zraka.
Ova analiza ukazuje da su redovan i neredovan zrak linearno polarizovani,ali
sa oscilacijama koje su uzajamno normlalne.
preuzmi
seminarski rad u wordu » » »


