OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
Svetlost, difrakcija i polarizacija
Optika je deo fizike koji proučava svetlosne pojave i prirodu svetlosti. Vidljiva svetlost je elektromagnetno zračenje koje opaža organ vida – oko. Optika izučava pojave vezane vezane ne samo za vidljivi deo spektra zračenja, nego i one vezane za infracrveno i ultraljubičasto (ultraviolentno) zračenje.Optika se prema načinu tretiranja optičkih pojava može podeliti na dve osnovne oblasti: geometrijsku i fizičku optiku. Geometrijska optika proučava optičke pojave na temelju osnovnih zakona koji su empirijski. Ne razmatra pitanja o prirodi svetlosti , za razliku od fizičke optike koja proučava prirodu svetlosti i kroz to objašnjava probleme nerešive u geometrijskoj optici.
SVETLOST – elektromagnetno zračenje
Šta je svetlost? Npr., za Njutna
svetlost je bila struja čestica, dok je za Hajgensa svetlost slična talasima
na vodi. Na osnovu ovih teorija mogu se objasniti neki jednostavni optički
zakoni kao što je zakon polarizacije. Međutim, novi elektromagnetni
rezultati su išli u prilog talasne teorije.
Svetlost možemo opisati kao roj čestica koje se nazivaju fotoni.
Svaki foton nosi određenu količinu energije. Celokupan raspon zračenja
koje nastaje u svemiru nazivamo svetlosni spektar.
Vrste elektromagnetskog zračenja:
- gama zračenje
- rendgensko zračenje (X-zraci)
- ultraljubičasto zračenje
- vidljivo zračenje (svetlost)
- infracrveno zračenje
- mikrotalasno zračenje
- radiotalasi
Elektromagnetska zračenja uzajamno se razlikuju jedino frekvencijom.
Svetlost nastaje kada se električni naboj kreće u elektromagnetskom polju.
Atom šalje svetlost kada je neki od njegovih elektrona podstaknut dodatnom
energijom izvora. Zračenje pokrenutih elektrona opisujemo talasom. Svetlost
manje energije ima manju učestalost ili frekvenciju, ali vecu talasnu
dužinu, dok ona sa više energije ima veću učestalost ili frekvenciju,
ali manju talasnu dužinu.
Brzina svetlosti, kao i svih ostalih elektromagnetnih talasa iznosi oko
299 792 500 m/s.
Boja
Ljudsko oko reaguje samo na ograničeni raspon talasnih
dužina na vidljivu svetlost, ali ono odlično raspoznaje i vrlo male razlike
unutar tog raspona. Te male razlike nazivamo bojama. Boje su, dakle, male
frekvencijske razlike u području vidljive svetlosti. Najkracu talasnu
dužinu imaju ljubičasta i plava svetlost, a najdužu crvena svetlost.
Spektar vidljivog zračenja čine:
- ljubičasta boja (najveća frekvencija najkraća talasna dužina)
- plava boja
- zelena boja
- zuta i narandžasta boja
- crvena boja
Bela svetlost sastavljena je od kontinuiranog niza svih boja vidljivog
spektra. U praksi pod bojom nekog tela možemo smatrati boju koju telo
reflektuje kada osvetljeno belom svetlošću, odnosno telo će biti obojeno
nekom bojom ako površina apsorbira belu svetlost samo na odredjenom talasnom
području.
Boja, dakle, zavisi od frekvencije reflektiranog zračenja. Bela površina
je ona koja u jednakoj meri reflektuje sva talasna područja bele svetlosti.
Crna površina je ona koja u potpunosti apsorbuje belu svetlost. Mi gledamo
vidljivu svetlost iz dva razloga:
- Zrak je poziran na vidljivu svetlost za razliku od drugih stvari, pa tako svetlost prolazi kroz atmosferu do nas.
- Sunce isijava najviše energije upravo u vidljivom delu spektra. Vruća zvezda produkuje većinu svetlosti u ultraljubičastom području, dok hladna zvezda većinu svetlosti produkuje u infracrvenom području.
Pa tako, Sunce, prosečna zvezda produkuje većinu energije u vidljivom delu spektra.Sve boje koje vidimo na Zemlji i negde drugo su samopitanje koje se talasne dužine sunčeve svetlosti najbolje reflektuju.
Izvori svetlosti
Svetlosnio izvori su tela koja stvaraju svetlost. Svetlost se od izvora na sve strane rasprostire pravolinijski. Ppavci po kojima se rasprostire svetlost nazivaju se svetlosni zraci. Deo prostora iza svetlosnog tela nasuprot svetlosnom izvoru u koji ne dolazi nepostedna svetlost izvora naziva se senka. Odbijanje svetlosti naziva se refleksija, a prelamanje svetlosti naziva se refrakcija. Razlaganje bele svetlosti je disperzija.
Dopplerov efekat
Dopplerov efekat je promena posmatrane talasne dužinezbog medjusobnog približavanja ili udaljavanjaizvora talasa i posmatrača. Talasne dužine linija povećavaju se (pomiču prema crvenom području spektra) kada se izvor udaljava, a smanjuju se (pomiču prema plavom području spektra) kada se izvor priblizava posmatraču.
TALASNA OPTIKA
Osnovni pojam geometrijske optike je zrak svetlosti, a fizikalne optike je talas svetlosti. Sve do sada posmatrane i proučavane pojave se mogu izvesti iz tri osnovna zakona koja za geometrijsku optiku imaju karakter aksioma, a to su:
- Zakon pravolinijskog širenja svetlosti
- Zakon refleksije
- Zakon loma
Ta tri zakona, a prema tome i sve pojave koje se pomoću njih mogu izvesti,
mogu se protumačiti sa dve potpuno različite teorije.
- Pevu teoriju, tzv. korpuskularnu, postavio je Newton i glasi: Svetlost
se sastoji od sitnih korpuskula (čestica), tzv. fotona koje izlaze velikom
brzinom iz izvora svetlosti.
- Drugu teoriju, koja se zove talasna teorija, postavio je Huygens i glasi:
Svetlost je osciliranje koje se iz izvora svetlosti širi u obliku talasa,
a raznim bojama pripadaju oscilaciji različite frekvencije.
Kada se govori o prirodi svetlosti kaže se da je svetlost dvojne prirode:
nekad se ponaša kao elektromagnetni talas, a nekada kao snop čestica-fotona.
Talasne osobine svetlosti su najočitije u pojavama interferencije, difrakcije
i polarizacije. Interferencija i difrakcija su pojave karakteristične
za sve vrste talasa, na primer, talase na vodi, zvučne talase itd. Interferenciju
i difrakciju svetlosnih talasa moguće je ostvariti samo u posebnim uslovima.
Pojava polarizacije svetlosti je povezana sa transverzalnošću svetlosnih
talasa. Vektor električnog polja (E), čije oscilacije odredjuju fiziološka,
fotehemijska, fotoelektrična i druga delovanja svetlosti, oscilira u ravni
u odnosu na pravac prostiranja svetlosnog talasa. Ako je to osciliranje
uredjeno na odredjeni način dolazi do pojave polarizacije svetlosti.
Talas je periodični poremećaj u prostoru. Da nastane talas treba postojati
neki izvor. Razlikujemo dve vrste talasa s obzirom na način širenja kroz
prostor:
- Progresivni ili putujući talas
- Longitudinalni talas
Tipični primer progresivnog talasa je talas na površini vode. Površina
vode se diže i spušta dok se breg giba uzduž površine, dolazi do oscilacija
molekula vode u odnosu na smer širenja talasa tj. na smer gibanja brega.
Takav talas naziva se transvezalni talas jer je pomak
čestica uspravan na smer gibanja talasa.

Još jedan primer transvezalnog talasa je elektromagnetni talas. Kod elektromagnetnog
talasa električno i magnetno polje menjaju se periodično s vremenom u
smerovima u odnosu na smer gibanja talasa, tj. na smer prenosa energije.
Osim transverzalnih talasa postoje i longitudinalni talasi. To su talasi
kod kojih dolazi do oscilacije čestica u smeru širenja talasa. Primer
longitudinalnog talasa je zvuk, tj. zvučni talas. Od izvora zvuka molekule,
atomi osciluju oko ravnotežnog položaja na pravcu širenja talasa.
Elementi talasa:
Brzina širenja |
koliki put predje neka tačka talasa u jefinici vremena |
frekvencija |
broj oscilacija u jednoj sekundi |
Talasna dužina |
razmak najbližih tačaka koje osciluju u fazi |
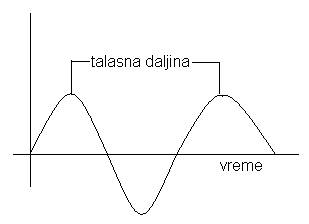
Relacija koja povezuje ova tri elementa talasa je:
v = l x f
Brzina talasa jednaka je proizvodu talasne dužine i frekvencije.
DIFRAKCIJA SVETLOSTI
Zakoni geometrijske optike su izvedeni pod predpostavkom
da se svetlost prostire pravolinijski. Medjutim, ako na svom putu svetlost
pada na tela ili otvore malih dimenzija, koji se mogu porediti sa talasnom
dužinom svetlosti, tada se javljaju pojave difrakcije (savijanja) svetlosti.
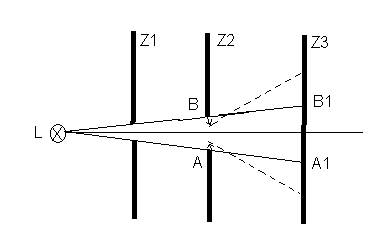
Na primer, ukoliko se bela svetlosttačkastog svetlosnog izvora L propusti
kroz pukotinu zaklona Z1 i kroz paralelno postavljenu drugu pukotinu Z2,
tada se na zaklonu Z3 vidi slika pukotine AB, odnosno A1B1 kao posledica
pravolinijskog prostiranja svetlosti. Medjutim, ako se pukotina na zaklonu
Z2 poširini smanji, na zaklonu Z3 levo i desno od centralnog luka, zapažaju
se obojene pruge, isprekidane tamnim medjuprostorima. Ukoliko se pukotina
i dalje sužava, svetlosno područje izmedju Z2 i Z3 se širi, a intezitet
linija opada sa udaljavanjem od centralnog lika. Očito je da svetlost
u ovom slučaju odstupa od pravolinijskog prostiranja, tj. da po izlasku
iz sužene pukotine skreće (savija).
Slično se dešava ako svetlost naidje na uske prepreke. U oba slučaja,
obojene pruge nastaju kao posledica interferencije savijene svetlosti.
skretanje svetlosnih zraka od pravolinijskog prostiranja naziva se difrakcija
ili savijanje vetlosti.
Zraci svetlosti koji padaju na pukotinu mogu biti paralelni, ili mogu
padati pod odredjenim uglom. Ako su na celokupnom putu od izvora do ekrana
zraci paralelni, nastaje difrakcija Frauhoferovog tipa. Kod difrakcije
Frenelovog tipa zraci mogu biti divergentni ili konvergentni. Pojavu difrakcije
redovno prati pojava interferencije izmedju savijenih svetlosnih zraka,
izmedju kojih postoji odredjena putna (fazna) razlika.
Potrebno je istaći da se pojava difrakcije bitno razlikuje od prelamanja
svetlosti. Prilikom prelamanja, promena pravca upadnog talasa dešava se
na granici dve fizičke raznorodne sredine, različitih optičkih gustina.
na toj se granici menjaju brzina prostiranja talas i njegova talasna dužina.
Difrakcija se odigrava prilikom prostiranja u jednoj istoj sredini, kada
talas u svom kretanju samo „zakači“ granicu izmedju sredine.
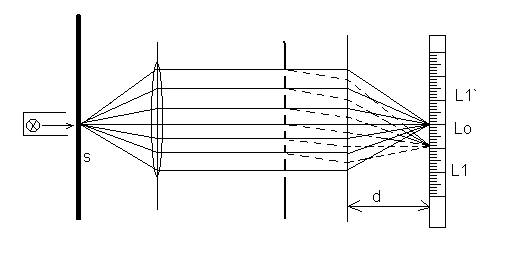
Difrakcija na pukotini
Nastanak difrakcione slike pri prolasku svetlosti kroz pukotinu može da se objasni pomoću Hajgensovog principa.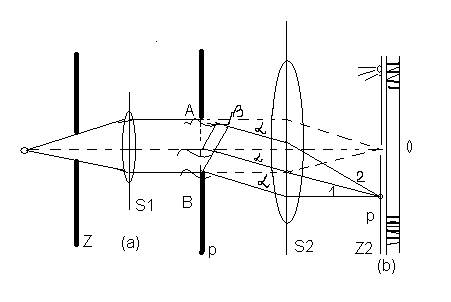
Posmatrajmo tačkasti izvor svetlosti koji se nalazi u žiži sočiva S1 i emituje monohromatsku svetlost. Svetlost se pomoću zaklona Z usmerava na sabirno sočivo S1 na kojem se prelama.Prelamanjem nastaju paralelni zraci koji padaju na pukotinu p, koja je na slici prikazana znatno uvećana.Prema Hajgensovom principu, svaka tačka pukotine postaje izvor novih svetlosnih talasa koji padaju na sočivo S2 i sakupljaju se na zaklonu Z2. Svi paralelni zraci koji napuštaju pukotinu pod odredjenim uglom a, fokusiraju se u jednu tačku na zaklonu. Na ovaj se način, usled difrakcije na pukotini p, na zaklonu stvarainterferenciona slika (slika b), koja se sastoji od široke svetle trake na sredini (a=0) i okružena je nizom svetlih i tamnih mesta.Svetlost koja stiže do sočiva S2 sastoji se od velikog broja ravnih talasa. Svi ovi talasi su koherentni (potiču iz istog izvora) i uzajamno se razlikuju samo po fazama. Fazna razlika izmedju paralelnih ravnih talasa koji se prostiru pod uglom a nastaje usled njihove putne razlike.
Difrakcija na rešetki
Difrakcija se javlja i na nizu paralelnih pukotina. Sistem od velikog
broja bliskih paralelnih pukotina naziva se difrakciona rešetka. Optičke
difrakcione rešetke se uglavnom izradjuju od staklenih planparalelnih
ploča na koje se na jednakim rastojanjima nanosi velik broj tankih zareza
(do 2400 na 1mm).
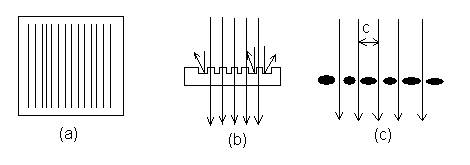
Svetlost se sa zarezima difuzno rasejava, dok se prostor izmedju zareza
ponaša kao pukotina koja propušta zrake. Rastojanje izmedju susednih pukotina
c naziva se konstanta rešetke. Ako je širina svake pukotine d, a širina
zareza d0, tada je:
c = d + d0
Optičke difrakcione rešetke se mogu urezati i na konkavnim ogledalskim
površinama (Rolandove refleksione rešetke) i tada se difrakcija stvara
od svetlosnih zraka koji se reflektuju sa ogledalskih površina izmedju
zareza. Usled velikog broja pukotina, rešetka propušta puno svetlosti
i stvara dobro osfetljenu sliku interferencije.
Uvećana slika dela jedne transmisione difrakcione rešetke sa N pukotina
prikazaću na sledećoj slici. Inerferenciona slika kd rešetke nastaje usled
difrakcije na svakoj pukotini, kao i usled interakcije izmedju N snopova
svetlosti koji nastaju na pukotinama. Zbog toga se raspodela inteziteta
svetlosti u interferencionoj slici rešetke I (a) dobija kao proizvod raspodele
inteziteta usled difrakcije na jednoj pukotini Ip (a) i raspodele inteziteta
zbog interferencije N snopova IN (a):
I (a) = Ip (a) IN (a)
Ovde se razmatra o raspodeli intenziteta monohromatske svetlosti usled
medjusobne interferencije snopova svetlosti koji nastaju na svakoj pukotini.
Svaki snop iz jedne pukotine koji dolazi pod uglom a se opisuje jednačinom
oblika, odnosno vektorom aai. Na slici možemo
zapaziti da je putna razlika izmedju susednih snopova:
d = c sin a
Poližaj glavnih maksimuma u raspodeli IN (a):
sin a = k l/c a= arcsin k l/c
sin a = -k l/c a= arcsin k l/c
Minimumi odgovaraju uglovima:
a = arcsin kl/cN
a = -arcsin klcN
Brojna vrednost konstante k u relaciji odredjuje red interferencije.
Prema tome, razlikuju se interferentni maksimumi prvog k=1, drugog k=2,...
reda. Sa povećanjem reda interferencije visina maksimuma opada.
Položaj interferentne slike zavisi od talasne dužine svetlosti. Ako se
rešetka ozrači složenom (polihromatskom) svetlošću, ona se u interferentnoj
slici razlaže na komponente. Oko nultog maksimuma koji ostaje nerazložen
(jer za k=0, položaj maksimuma je a=0, nezavisno od l) simetrično se javljaju
spektri svetlosnog izvora (sledeća slika) u pojedinim redovima interferencije.
U ovim spektrima ljubičasti (kratkotalasni) deo savija manje od crvenog
(dugotalasnog) dela. Savijanje (skretanje) je direktno srazmerno talasnoj
dužini, pa se zato kaže da rešetka daje normalan spektar (ima linearnu
disperziju).
U optičkoj spektoriskopiji se često koristi rašetka za merenje talasne
dužine i intenziteta spektarnih linija. Ako je konstanta rešetke c poznata,
može se merenjem ugla skretanja a odrediti talasna dužina spektralne linije.
Kod istraživanja složenih spektara veoma važna karakteristika rešetke
je moć razlaganja. Moć razlaganja D pokazuje na koji ugao može rešetka
razložiti dve bliske spektralne linije i definiše se relacijom:
D = da / dl
Moć razlaganja rešetke se može izrčunati diferenciranjem relacije što daje:
cosada = k/c dl
odakle se dobija:
D = k/c cosa – Moć razlaganja
Za male uglove a može se primetiti aproksimacija cos a![]() 1,
pa se moć razlaganja može izraziti relacijom:
1,
pa se moć razlaganja može izraziti relacijom:
D ![]() k/c
k/c
Kao što se vidi na osnovu dobijenih ralacija, moć razlaganja rešetke
se povećava smanjenjem konstante rešetke. Moć razlaganja rešetke se povećava
i redom interferencije. Medjutim, spektri višeg reda su obično veoma slabog
intenziteta i mogu se uzajamno prekrivati.
U poredjenju sa disperzijom svetlosti kroz prizmu, rešetka daje bolje
razložen, normalan spektar. Disperzija u slučaju prizme nije linearna,
svetlosni zraci kraće talasne dužine skreću više.
Difrakcija talasa (valova) na vodi
Difrakcija je karakteristična za talase na vodi. Difrakcija
talasa se može primetiti gledajuci morske talase kako nailaze na primer
na drvene stubove u vodi i slično.
Evo jednog malog eksperimenta sa talasima na vodi. Pomoću grafoskopa na
kojeg smo stavili posudu sa vodom na čijem se kraju nalazi vibrator sa
pločastim nastavkom (pomoću kojeg proizvodimo talase na vodi). Posmatraćemo
difrakciju talasa na vodi. Stavimo li na put talasa prepreku (npr. neku
malu pukotinu) nakon prolaska kroz nju talasi se ugibaju u području senke.
(krugovi na slici 7). Difrakcija se lakše uoči što je pukotina uža. Ako
je pukotina jednaka talasnoj dužini iza pukotine talasi se šire tako da
zapravo vidimo geometrijski senku pukotine (slika 7).
Difrakcija X-zraka
X-zrake je otkrio Rentgen 1895. godine, pa se oni danas nazivajurendgenski
zraci. To su zraci elektromagnetne prirode, talasna dužina im se nalazi
u intervalu 0,001 nm do 10 nm, a javljaju se na mestima gde se brzi elektroni
naglo koče. To se obično postiže pomoću vakumske rendgenske cevi.
S obzirom na malu talasnu dužinu rendgenskih zraka, njihova se interferencija
nije mogla dobiti nikakvom načinjenom rešetkom. Laue je došao na pomisao
da bi kristali mogli poslužiti kao difrakciona prostorna rešetka za X-zrake.
Pravilno rasporedjeni atomi u kristalu čine rešetku, na kojoj se davlja
primetna difrakcija X-zraka.
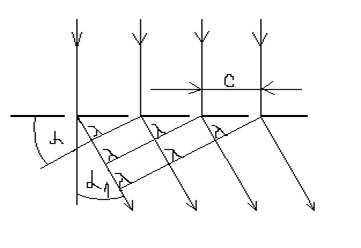
Breg je jednostavno objasnio pojave difrakcije X-zraka putem refleksije
na pojedinim ravnima rešetke. Horizontalne linije predstavljaju ravni
kristala na koje pada uzak snop zraka. Ugao izmedju zraka i ravni naziva
se ugao sjaja. Na svakoj se ravni jedan deo upadnog zračenja odbija po
zakonima odbijanja i svi nizovi talasa odbijenih od ravni pod uglom nalaze
se u fazi.Intenzitet odbijenog zraka može biti primetan samo u slučaju
ako se, usled interferencije sa zracima odbijenih od susednih ravni, pojača.
Ovo nastupa u slučaju ako su talasi (zraci) medjusobno u fazi, odnosno
ako im je putna razlika jednaka celom broju talasnih dužina.
Difrakcija X-zraka (i neutrona) na kristalima može se koristiti ne samo
za merenje talasnih dužina rendgenskih zraka, nego i za rešenje obrnutog
zadatka: za odredjivanje strukture kristala pri korišćenju zraka poznatih
talasnih dužina. Detaljno izračunavanje oblika difrakcionih slika na raznim
kristalima omogućava da se utvrdi geometrijski tip njima odgovarajućih
rešetki. Ispitivanja ove vrste razvila su se danas u samostalnu granu
fizike, poznatu pod nazivom rendgenska strukturna analiza. Rendgenska
strukturna analiza nalazi široku primenu i u kristalografiji i u tehnici,
gde predstavlja važan metod za izračunavanje svojstava materijala (čelika,
legura obojenih metala itd.).
POLARIZACIJA SVETLOSTI
Interferencija i difrakcija svetlosti su pojave koje potvrdjuju da je
svetlost talasne prirode. Medjutim, oni ne daju odgovor na pitanje da
li su svetlosni talasi transferzalni ili longitudinalni. U transferzalnom
talasu, koji se prostire u pravcu aa’, sve tačke optičke sredine
izvode oscilacije u odredjenoj ravni AB.
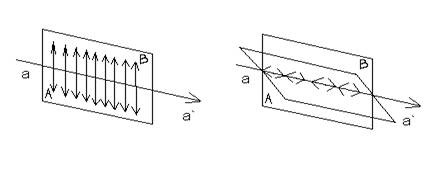
Prema tome, transverzalni talas u odnosu na razne ravni postavljene kroz
pravac njegovog prostiranja, ima različita svojstva. U longitudinalnom
talasu, medjutim, oscilacije se vrše duž pravca prostiranja talasa aa’
i njegova svojstva su ista u odnosu na bilo koju AB, postavljenu kroz
pravac njegovog prostiranja. Pojava polarizacije svetlosti daje nedvosmislen
dokaz da je svetlost transverzalni elektromagnetni talas.
Pod pojavom polarizacije podrazumeva se proces takvog uzajamnog dejstva
prirodne svetlosti i neke materijalne sredine, pri kojem se prirodna svetlost
pretvara u polarizovanu svetlost. Eksperimentalno je utvrdjeno da se svetlost
sastoji od transverzalnih elektromagnetnih talasa sa uzajamno normalnim
vektorima električnog i magnetnog polja koji su normalni na pravac prostiranja
svetlosti. Svetlosni talas koji je emitovan od strane jednog odredjenog
atome svetlosnog izvora u jednom aktu emisije (prelaskom elektrona sa
pobudjenog na osnovno stanje atoma) ima važnu osobinu da mu vektor električnog
polja osciluje u strogo odredjenoj ravni, a veltor magnetnog polja takodje
u odredjenoj ravni. Talas ovakvih osobina naziva se linearno polarizovan
talas, jer u bilo kojoj tački duž njegovog prostiranja vektori električnog
i magnetnog polja zadržavaju polaznu ravan oscilovanja.Vektor jačine električnog
polja naziva se svetlosni vektor i koristi se za opis pojava u optici.
Ravan u kojoj osciluje vektor električnog polja naziva se ravan oscilovanja
svetlosnog talasa. Kod linearno polarizovane svetlosti, ravan normalna
na ravan oscilovanja svetlosnog vektora naziva se polarizaciona ravan.
Svaki realni izvor svetlosti sastoji se iz velikog broja atoma i molekula,
koji zrače svetlosne talase potpuno neuredjeno, sa svim mogućim orjentacijama
ravni oscilovanja, normalnih na pravac prostiranja. Ovakva svetlost nije
polarizovana i naziva se nepolarizovana ili prirodna svetlost. Izmedju
faza pojedinih talasa ne postoji nikakva veza, one su haotično rasporedjene.
Kod linearno polarizovane svetlosti svetlosni vektor menja intenzitet
i smer, a pravac mu ostaje isti.
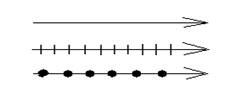
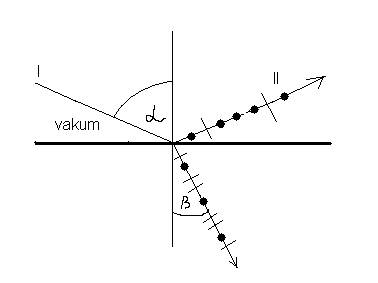
Da bi se na crtežima polarizovani zrak razlikovao od prirodnog, usvojeno
je da se: prirodni zrak predstavlja pravom linijom, linearno polarizovani
zrak čija se ravan oscilovanja poklapa sa ravni crteža predstavlja kao
prava linija sa crtiacama, a ako je ravan oscilovanja normalna na ravan
crteža, označava se pravom linijom sa tačkama.
Svetlost može biti delimično linearno polarizovana (kada sadrži talase
pretežno sa svetlosnim vektorom orijentisanim u jednom pravcu, a manji
broj u ostalim pravcima), kao i cirkularno i eliptično plarizovana. Linearno
polarizovana svetlost se može dobiti na više načina kao što su: odbijanje,
dvojno prelamanje, selektivna apsorpcija rasejanjem, prolaskom svetlosti
ili njenim prelamanjem kroz optički anizotropna tela ( ona tela čija su
optička svojstva (brzina prostiranja svetlosti, indeks prelamanja i dr.)
različita u različitim pravcima) itd.
Polarizacija svetlosti odbijanjem
Kada se svetlosni zrak spusti pod izvesnim uglom a na graničnu površinu vazduh-providna sredina, on se jednim delom odbija, a drugim prelama na osnovu zakona prelamanja, odnosno odbijanja. Odbijeni i prelomljeni zrak su pri tome delimično linearno polarizovani, a njihove ravni polarizacije stoje medjusobno normalno ( odbijeni zrak je polarizovan u ravni koja je normalna na upadnu ravan, dok je prelomljeni zrak polarizovan u ravni koja je paralelna upadnoj ravni.
Dvojno prelamanje
Ako se slova posmatraju kroz kristal islandskog kalcita, CaCO3, vide
se udvojena. Obrtanjem krostala jedna slika miruje, dok se druga obrće
u krug zajedno sa kristalom. Ista se pojava opaža, ako se uzak snop paralelne
svetlosti propusti kroz kristal islandskog kalcita. Na zaklonu se vede
dva lika: jedan u prvobitnom pravcu, a drugi pomeren u stranu. Obrtanjem
kristala oko zraka ovaj ostaje nepokretan, a drugi se obrće oko njega.
Iz ovoga se može zaključiti da kristal deli prirodan zrak na dva dela,
zraka koji se različito prelamaju. Prvi se prelama po zakonima prelamanja
i naziva se redovan zrak, a drugi odstupa od ovih zakona i naziva se neredovan
zrak.
Ako se kroz kristal propusti linearno polarizovana svetlost, likovi su
u opštem slučaju, različitog intenziteta. Obrtanjem kristala za 360 stepeni,
intenzitet likova se menja od maksimalne vrednosti do gašenja i to tako
da je jedan ugašen, kada drugi ima maksimalan intenzitet. Iz ove se analize
može ustanoviti da su oba zraka, redovan i neredovan, linearno polarizovana
i da su njihove polarizacione ravni medjusobno normalne.
Dvojno prelamaju islandski kalcit, turmalin, kvarc, herapatit i mnogi
drugi providni kristali.
Pojave dvojnog prelamanja su posledice kristalne strukture. Optičke
osobine kristala nisu u svim pravcima jednake, i brzina svetlosti zavisi
od pravca svetlosnog zraka u kristalu. Jedino u pravcu optičke ose kristala
redovan i neredovan zrak imaju jednaku brzinu, a u svim ostalim pravcima
njihove su brzine različite. Prema tome i indeks prelamanja je u pom slučaju
jednak za oba zraka u pravcu optičke ose, a tada se, logično, upadni zrak
ne udvaja.
Prema Hajgensu, šematski su prikazave (prva slika) brzine redovnog i neredovnog
zraka iz jedne tačke 0 u kristalu kalcita. Kako su te brzine različite
na sl. krug i elipsa predstavljaju preseke površine lopte i rotacionog
elipsoida do kojih su dospeli talasi redovnog i neredovnog zraka. Loptasta
površina pripada redovnom, a elipsoidna neredovnom zraku.
U pravcu optičke ose talasi redovnog i neredovnog zraka stižu do jednake
udaljenosti (pravac ose ne treba zameniti sa pravom). Prema tome, u pravcu
ose oba zraka imaju jednaku brzinu. Kao što se vidi redovan zrak ima u
svim pravcima jednaku brzinu, i njegove su talasne površine sferne. On
se ponaša po zakonu prelamanja i njegov indeks prelamanja (1,65) je konstantan
za svaki upadni ugao.
Brzina neredovnog zraka je promenljiva, njegove talasne površine su elipsoidi.
Jasno je i da je njegov indeks prelamanja promenljiv. Najveća vrednost
indeksa prelamanja je u slučaju kada zrak prolazi paralelno optičkoj osi,
ona je tada jednaka vrednosti indeksa prelamanja redovnog zraka (1,65).
Najmanji indeks prelamanja javlja se u slučaju kada je pravac upadnog
zraka normalan na pravac optičke ose. Prema tome, indeks prelamanja neredovnog
zraka zavisi od upadnog ugla i u slučaju kada svetlost pada u pravcu optičke
ose (prva slika), jedino se onda zrak ne deli.
Kristali koji imaju jednaku optičku osu nazivaju se jednoosni ( kristali
tetragonalnog i heksagonalnog sistema). Znači, kristal islandskog kalcita
je optički jednoosan.
Kristali koji imaju dve optičke ose, a to znači da imaju dva pravca u
kojima je brzina prostiranja jednaka, nazivaji se optički dvoosni. Takvu
osobinu imaju kristali rombičnog i monokliničkog sistema. Nijedan od dva
razdeljena zraka se ne ponaša po Dekart-Snelijusuvom zakonu prelamanja.
Kod kristala islandskog kalcita zapaža se da je brzina prostiranja veća,
a indeks prelamanja manji, za neredovni zrak u odnosu na redovni (prva
slika).
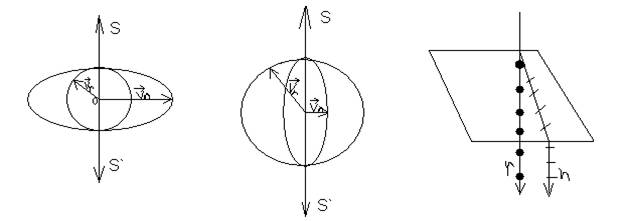
Postoje jednoosni kristali, npr. kvarc kod kojih je stvarna brzina redovnog
zraka veća, a njegov indeks prelamanja manji u odnosu na neredovan zrak.
U prvom slučaju kristali pokazuju negativno dvojno prelamanje (prva slika),
a u drugom slučaju pozitivno (druga slika). Dvojnim prelamanjem prirodne
svetlosti dobijaju se linearno polarizovani izlazni zraci, kod kojih su
ravni oscilovanja redovnog i neredovnog zraka medjusobno normalne (treća
slika). Kako su izlazni zraci blizu jkedan drugom, da bi se polarizovana
svetlost dobijena dvojnim prelamanjem mogla koristiti, jedan od ova dva
zraka mora se ukloniti.
1. Nikolova prizma. Otklanjanjem jednog od dva zraka engleski fizičar
Nikol je postigao pomoću prizme, koja je po njemu nazvana Nikolova prizma.
Osnove kristala islandskog kalcita se izbruse tako da se bočnim stranama
obrazuje ugao od 68 stepeni. Kristal se zatim prereže po ravno Ac koja
je normalna na obe osnove. Na slici je prikazan uzdužan presek Nikolove
prizme.
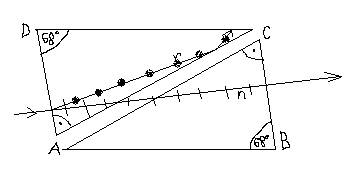
Kada na ovakvu prizmu pada prirodan zrak, tada se deli na redovan i neredovan.
Indeks prelamanja za redovan zrek je veći (1,658), a za neredovan je manji
(1,468) od indeksa prelamanja kanada-balzama (1,53). Kako redovan zrak
pada na kanada-balzam pod većim upadnim uglom od graničnog ugla (68 stepeni),
on se od sloja kanada-balzama totalno reflektuje i odvaja od neredovnog
zraka. Prema indeksu prelamanja (1,658) redovnog zraka vidi se da je kalcit
za njega optički gušća sredina od kanada balzama, zbog čega i dolazi do
totalne refleksije. Neredovan zrak za koji je kalcit optički redja sredina
od kanada-balzama, prolazi kroz prizmu i kao linearno polarizovan izlazi
iz nje. Redovan zrak je apsorbovan slojen crne boje kojom je premazana
prizma. Na ovaj se način, dvojnim prelamanjem, dobija linearno polarizovana
svetlost.
Neki kristali (turmalin, hepatit, jod-kinin i dr.), pored dvojnog prelamanja,
imaju osobinu da jedan polarizovani zrak više apsorbuju od drugog, pa
se na taj način takodje može dobiti polarizovana svetlost.
Optički sistem koji polarizuje prirodnu svetlost naziva se polarizator,
a sistem kojim se utvrdjuje da je svetlost polarizovana naziva se analizator.
Ako je osa analizatora paralelna osi polarizatora polarizovana svetlost
prolazi kroz analizator. Kada ose polarizatora i analizatora obrazuju
prav ugao (ukršteni položaji), polarizovana svetlost ne može da prodje
kroz analizator, jer je u celini apsorbovana u amalizatoru. Kada su ose
polarizatora i analizatora pod proizvoljnim uglom f, kroz analizator prolazi
samo deo svetlosti. Zavisnost intenziteta svetlosti propuštene kroz analizator
od ugla obrtanja analizatora f data je relacijom:
I = I0 cos f
gde je I0 intenzitet svetlosti koja pada na analizator. Ova relacija izražava Malusov zakon koji glasi: Intenzitet svetlosti koju propušta analizator srazmeran je kvadratu kosinusa ugla izmedju analizatora i polarizatora. Ovaj zakon se odnosi na relativni intenzitet svetlosti, tj. intenzitet po odbitku apsorpcije. Daljim obrtanjem analizatora proces se ponavlja. Ako se analizator obrne za p, svetlost se ponovo javlja, a za 3p/2 ponovo gasi itd.Polarizacija pomoću selektivne apsorpcije. Polaroidi
Izvesni kristali (npr. turmalin) imaju osobonu da osim razlaganja svetlosti
u redovan i neredovan zrak pokazuju i znatno veću apsorbciju za jedan
od njih. Ova pojava se naziva selektivna apsorpcija (dihroizam). Zrak
prirodne svetlosti (nepolarizovane) se probija kroz kristal, u kojem se
javlja dvojno prelamanje. Redovan zrak, ukoliko je put kroz kristal dovoljno
dug, biva potpuno apsorbovan., a neredovan prolazi kroz kristal veoma
malo apsorbovan. Na taj se način na izlaznoj strani kristala pretežno
dobija jedan polarizovan zrak.
Za dobijanje polarizovane svetlosti često se koriste polaroidi. Polaroid
sačinjava prozračan tanak film od želatina, u kojem su posebnim tehnološkim
postupkom ugradjeni veoma sitni igličasti kristali herapatita (kristala
kinin-jodsulfata). Iako ovi polaroidi daju samo približno linearno polarizovanu
svetlost, njihova je svetlost u tome što se mogu izraditi u dovoljno velikim
dimenzijama i ekonomičniji su za praktičan rad.
Obrtanje polarizacione ravni. Optička aktivnost
Gledajući kroz ukržtene Nikolove prizme monohromatsku svetlost, posmatrano
polje je tamno. Ako se izmedju njih stavi pločica od kvarca, sečena okomito
na optičku osu, polje posmatranja postaje svetlo. Da bi se gašenje ponovo
postiglo, analizator se mora obrnuti za izvestan ugao a. To znači da je
svetlost koja prolazi kroz pločicu ostala linearno polarizovana, ali da
se ravan oscilivanja, odnosno polarizaciona ravan u kvarcu obrnula za
izvestan ugao a. Taj se ugao naziva ugao obrtanja /rotacije) i on zavisi
od debljine pločice i od talasne dužine svetlosti.
Osobinu obrtanja polarizacione ravni osim kvarca imaju i neki drugi kristali,
zatim rastvori organskih materijala, na primer šećera, vinske kiseline
itd.Takvi se materijali nazivaju optički aktivne supstance. Neke od ovih
supstanci obrću polarizacionu ravan udesno, a neke ulevo, računajući smer
obrtanja prema tome u koju se stranu obrće analizator, da posmatrano polje
bude ponovo tamno. Neki kristali kvarca imaju desnu (desni kvarc), a neki
levu rotaciju (levi kvarc).
Obrtanje ravni oscilovanja nastaje usled asimetruje
molekula kod optički aktivnih supstanci. Asimetrička organska jedinjenja
sadrži atom ugljenika kod kojeg su za četiri veze vezane različite funkcionalne
grupe, kao na primer, kod mlečne kiseline (CH3-CHOH-COOH), grupe COOH,
OH, CH3
i H.
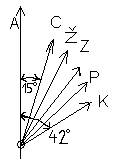
Ako se umesto monohromatske svetlosti propusti bela svetlost kroz pločicu
kvarca, svakoj talasnoj dužini odgovara drugi ugao obrtanja, i prema tome,
dobija se, za različite položaje analizatora različito vidno polje. Najmanji
je ugao nza crvenu (za kristal kvarca iznosi 15 stepeni), a najveći za
ljubičastu (za kristal kvarca iznosi 50 stepeni) svetlost (slično prelamanju
kroz prizmu). Na slici je prikazan ugao obrtanja polarizacione ravni različitih
talasnih dužina (crvene, žute, ..., ljubičaste) svetlosti, koja prolazi
kroz desni kristal debljine 1mm. OA je polarizaciona ravan bele svetlosti.
Obrtanjem analizatora za odredjeni ugao gasi se odgovarajućih boja i polje
je obojeno komplementarnom bojom. Ova se pojava naziva rotaciona disperzija.
Zavisnost ugla obrtanja od talasne dužine svetlosti slična je onoj za
indeks prelamanja svetlosti. Ako se ugao obrtanja ravni polarizuje po
jedinici dužine koju svetlost prodje kroz kristal označi kao specifična
moć rotacije i obeleži sa a, tada je:
[a] = M + N/l
gde su M i N konstante (date u tablicama).
Ugao obrtanja ravni polarizacije monohromatske svetlosti je srazmeran
dužini puta kroz optički aktivno telo. U čvrstim telima, na primer, ugao
obrtanja f je direktno srazmeran dužini d puta svetlosti:
f = [a]d
Specifična moć rotacije [a] zavisi od prirode supstance, temperature i
talasne dužine svetlosti. Za rastvore optički aktivnih supstanci važi
relacija:
f=[a]cd
gde je c koncentracija optički aktivne supstance u rastvoru.
Merenje ugla obrtanja ima značajnu praktičnu primenu. Na ovaj se način
odredjuje koncentracija aktivne supstance u rastvoru. Uredjaj za merenje
se naziva polarimetar. Uredjaji čija je skala kalibrisana da direktno
može da meri koncentraciju, na primer, rastvora šećera, nazivaju se saharimetri.
Literatura:
- Opšti kurs fizike, Beograd 1990. Dr Jevrem Jarić, Dr Nikola Cindro, Dr Ištvan Bikit
- Fizika, Zrenjanin 2003. Dr Vjekoslav Sajfert
- Internet stranice www.google.co.yu
preuzmi
seminarski rad u wordu » » »


