OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
POVIJEST FIZIKE
FIZIKA
je osnovna prirodna znanost (grč. physis,
priroda), unutar koje seistražuje i tumači materijalna stvarnost:
struktura i odnosi osnovnih sastojaka materije, na osnovi iskustvenih
činjenica i teorijskih istraživanja. Te se spoznaje oblikuju u shvatljive
principe (početne nazore), tzv. zakone fizike, koji se definiraju egzaktnim
matematičkim aparatom.
U vrijeme nastanka naše civilizacije, fizika, tzv. philosophia naturalis,
obuhvaćala je svu materijalnu stvarnost, no već su se u antičko doba iz
ove “prafizike” odvojile grane unutar kojih se proučavaju
posebni problemi: medicina, astronomija, kemija, geologija, biologija,
a u novije vrijeme različite grane tehnike. I danas je fizika, u užem
smislu, osnova svih grana prirodnih znanosti te je teško postaviti oštru
granicu između fizike kao osnovne znanosti i znanstvenih disciplina proizašlih
iz nje.
Do danas su se u jeziku zadržali tragovi sveobuhvatnosti fizike, npr.
doskora se u nas gradski liječnik zvao fizik, u engleskom je physician
liječnik, physic lijek, ljekarstvo, fizika je physics,
u francuskom je le physique vanjština (tjelesna), a la physique
je fizika.
Današnja fizika obuhvaća: klasičnu mehaniku, termodinamiku, elektrodinamiku,
optiku, zatim kvantnu mehaniku, statističku fiziku i elektrodinamiku,
nadalje teoriju relativnosti, atomsku i nuklearnu fiziku te fiziku subatomskih
čestica (koja opet obuhvaća niz specijaliziranih grupa).
Gotovo svaka od tih grana ima dva vida istraživanja, eksperimentalni i
teorijski, koji se često međusobno isprepliću i utječu jedan na drugi.
1 ANTIČKA FIZIKA
Već u prapovijesno doba čovjek je stjecao prva empirijska fizikalna znanja.
On je naučio da upotrebljava npr. polugu iako nije znao zakon na kojemu
se temelji njezina uporaba. Fizikalna znanja empirijski su se stjecala
i u prvim civilizacijama: Egiptu, Babilonu i Kini. Iako se tih empirijskih
znanja dosta nakupilo, ipak su ona interpretirana tek
u staroj Grčkoj. Tales (VII.
st. prije Krista), bez obzira na to što je raspolagao malom količinom
znanja, pokušao je naći me đusobnu povezanost pojava, a tvrdio je da je
sve proizišlo iz jednoga prvotnog počela – vode. Prapo čelo su tražili
i drugi Grci, pa se tako kao prapočelo isticao zrak ili vatra. Empedokle
(V. st. prije Krista) smatrao je da su četiri prapočela: zemlja, voda,
zrak i vatra, od kojih svako može imati i četiri kvalitete: toplo, vlažno,
hladno i suho. Pitagorejci su
napravili razliku između nebeskog područja, koje je savršeno i nepromjenljivo,
i zemaljskog, u kojemu je sve promjenljivo i nesavršeno. Tako je za ta
dva područja vrijedila i različita fizika. Demokrit je, naprotiv,
smatrao da se cijeli svijet sastoji od dvaju dijelova: punog i praznog.
Puni se sastoji od malih čestica koje su nedjeljive i nazivaju se atomi.
Svi fizikalni procesi nastaju zbog neprekidnog skupljanja i razdvajanja
atoma.
Prema Empedoklu, tijela se razdvajaju ili spajaju mržnjom i ljubavlju.
To su u biti sile, ali su shvaćene u psihološkom smislu. Silu je i Platon
(427. 347. g. prije Krista) shvaćao u psihološkom smislu. Prema
Platonu, postoji tendencija da se slično spoji sa sličnim. Zbog toga
i počela, zemlja, voda, zrak i vatra, zauzimaju svoja mjesta. Aristotel
(384. 322.g. prije Krista), slično Platonu, uzimao je da počela teže svom
prirodnom mjestu i takvo gibanje naziva se prirodnim gibanjem. Sva druga
gibanja su nasilna i potječu uvijek od sile kojoj je uzrok u prvom pokretaču.
Tako je za nasilna gibanja uvijek potrebna sila bez obzira na to kakvo
je gibanje. Prostor je za Aristotela
ograničen i pun. Aristotel prihvaća razliku zemaljskog i nebeskog područja
za koja vrijede različite fizike. Aristotelova fizika bila je kvalitativna
i spekulativna, ali je imala velik utjecaj na razvoj znanosti. Arhimed
(287. 212.), za razliku od Aristotela, uveo je u fiziku kvantitativne
odnose. Prvi je dao matematički zakon za polugu i matematički formuliran
zakon koji je kasnije nazvan Arhimedov
zakon.
2 SREDNJOVJEKOVNA FIZIKA
Aristotelova prirodna
filozofija, koja je uključivala i fiziku, bila je općenito prihva
ćena u srednjem vijeku. Čak i Roger Bacon (oko 1214. 1292),
koji je smatrao da je pokus mjerodavan za formiranje mišljenja o nekom
znanstvenom problemu i koji je tražio da se u znanosti eksperimentira,
bio je pristaša Aristotelove prirodne filozofije i svoje zaključke donosio
unutar nje. Ipak je u srednjem vijeku došlo do stanovitog napretka i
do novih znanstvenih rezultata. Dana su rješenja u različitim fizikalnim
područjima: optici, magnetizmu i u meteorologiji. Optika je doživjela
izvanredni napredak tijekom srednjeg vijeka, osobito u razdoblju 1250.
1350. Zanimanje za optičke probleme inicirao je arapski učenjak
Ibn al Haitan (965. 1039), koji je izvršio izvanredan utjecaj na
muslimanski Istok i latinski Zapad. Od optičkih problema opet se najviše
istraživao problem duge. Dietrich iz Freiberga, poznat i kao
Theodoric, dao je rješenje postanka dviju duga koje je gotovo
u potpunosti kasnije preuzeo Descartes. Problem plime uspješno
je rješavan u srednjem vijeku, pa su Giacomo Dondi i Zadranin
Federik Grisogono dali točan opis pojave plime i njene kvantitativne
odnose. U srednjem vijeku su rješavani i mnogi drugi fizikalni problemi,
ali gotovo svi u okviru Aristotelove tzv. peripatetičke prirodne filozofije.
Ipak, već u srednjem vijeku došlo je unutar te prirodne filozofije i
do znatnih udaljavanja od Aristotelova gledišta. Već je Filoponos,
koji je djelovao u prvoj polovini šestog stoljeća, smatrao da je dovoljno
da se na početku gibanja utisne u tijelo sila koja mu održava gibanje,
a da nije potrebno njezino stalno djelovanje izvana. Slično su tvrdili
Ing Sin (980. 1037) i Jean Buridan (XIII.-XIV. st.).
Prema Buridanu, tijelo dobiva na početku gibanja impetus koji održava
gibanje tijela. U srednjem vijeku napravljen je velik napredak i u izučavanju
kinematičkih svojstava gibanja. U tom pogledu osobito je važan Merton
College u Engleskoj u razdoblju između 1328. i 1350. U tom koledžu uvedena
je jasna distinkcija između dinamike i kinematike, definirano je jednoliko
ubrzano gibanje kao ono gibanje u koje se jednaki prirasti brzine postižu
u jednakim vremenskim razmacima, i dan je izraz za prijeđeni put kod
jednoliko ubrzanoga gibanja.
U srednjem je vijeku u fiziku uveden i pojam kvantitativne promjene. U staroj Grčkoj promjena se promatrala kao kvaliteta, a u srednjem vijeku počela se promatrati promjena topline, intenzitet svjetla, promjena brzine, akceleracije i gustoće, kao kvantitativna promjena. Neprekinutu promjenu brzine kod jednoliko ubrzanog gibanjaa grafički je predočivao Nicole Oresme (1323. 1382).
3 KLASIČNA FIZIKA
Novi vijek je obilježen pojavom novih pogleda na materijalnu stvarnost. Već je Nikola Kuzanski u XV. stoljeću tvrdio da je prostor beskonačan, a to su krajem XVI. stoljeća prihvaćali Giordano Bruno (1548. 1600.) i Franjo Petrišević s Cresa (1529. 1597.). Time je napušten Aristotelov pojam ograničenog prostora.
U XVI. stoljeću učenjaci su sve više napuštali kvalitativno promatranje fizikalnih pojava i sve više promatrali kvantitativne promjene i kvantitativne odnose. Kvantitativno promatranje fizike i uvođenje matematičke interpretacije bilo je uopće značajke renesanse.
Novu mehaniku, koja je bila bitno različita od peripatetičke, je početkom XVII. st. Galileo Galilei (1564. 642.). On je preuzeo sve rezultate koje su dobili prethodnici kritizirajući Aristotelovu prirodnu filozofiju. U prvom redu on, je prihvatio pojam impetusa i sve rezultate koje su dobili istraživači u Merton Collegeu. Njegova mehanika je temeljena na čisto matematič kim načelima. Galilei je matemtički izvodio svoje poučke iz nekih početnih tvrdnji, ali ih je potvrđivao i pokusom. Tako Galile izvodi poznati poučak da se prirasti putova kod jednoliko ubrzanoga gibanja odnose kao kvadrati proteklih vremena. Taj poučak Galilei je izvodio iz Oresmeovih i Buridanovih tvrdnji matematičkim putem, ali i potvrđivao eksperimentalno. Galilei je dobro definirao gibanje koje je posljedica kosog izbacivanja tijela. On je držao da je to složeno gibanje. Osim toga, Galilei je kod slaganja gibanja upotrebljavao načelo ustrajnosti iako ga nije dobro formulirao. Taj pojam strože je definirao Descartes. Galilejeva mehanika bila je samo kinematika, on nije htio raspravljati o sili, smatrajući taj pojam nejasnim.
Rene′ Descartes (1596. 1650.) odbacio je pojam sile i umjesto njeg uveo pojam vrtloga. Naime, po Descartesu je prostor ispunjen eterom, a u tom eteru postoje vrtlozi koji su uzrok gibanja. Descartes je definirao i pojam održanja gibanja što je bio prvi zakon održanja jedne fizikalne veličine. Taj zakon zajedno s pojmom vrtloga postavio je Descartes u temelj svoje fizike. Pojam punog prostora i vrtloga u fluidima bili su važni u fizici XVIII. st.
U XVII. st. postalo je jasno da zemlja, voda, zrak i vatra nisu počela jer se mogu dalje rastavljati. Oštru kritiku tih počela dao je Robert Boyle (1627. 1691). Umjesto tih počela, znanstvenici su sve više prihvaćali Demokritov atomizam koji je bolje odgovarao općim atomističkim shvaćanjima u matematici i fizici toga doba. Na temelju atomističkog shvaćanja i Boyleove kritike tražio se tada model strukture tvari. Stvaranju tog modela pomogli su Boyleovi pokusi s plinovima, a plin je bio vrlo prikladan da se na njemu promotri model strukture tvari, jer se mogao stlačiti, a i ekspandirao je ako nije bio u tome spriječen. Izneseno je više teorija koje se mogu podijeliti na one koje pretpostavljaju statički model plina i one koje predlažu kinematički.
Isaac Newton (1642. 1727.) dao je statički model udaljenih čestica među kojima djeluje sila. Prema kinematičkom modelu su čestice u silnoj uzbuđenosti te jure kroz prostor ispunjen vrlo finim fluidom. Pod utjecajem Descartove fizike znanstvenici su držali da gibanje čestica dolazi od vrtloga u tom fluidu.
Peripatetička i atomistička shvaćanja odražavala su se i u XVII. st. i na shva ćanje prirode svjetlosti. Aristotel je držao da je svjetlost val, a Demokrit je smatrao da se kroz prostor šire čestice koje prenose svjetlost. Jedno i drugo gledište prihvaćeno je u XVII. stoljeću. Descartes je prihvatio prirodu svjetla kao vala koji se širi kroz fluid, a Christian Huygens (1629. 1695) na tom je temelju izgradio svoju teoriju čestica tei na temelju toga zasnovao svoju korpuskularnu teoriju svjetlosti.
Newtonova mehanika. Newton je dovršio proces stvaranja nove prirodne filozofije, odnosno fizike. U prvom redu, on je na temelju Keplerovih gledišta o privlačenju među tijelima i drugih nastojanja u XVII. st. formulirao opći zakon gravitacije. Iz njega je matematički izveo Keplerove zakone i to je smatrao dokazom da je pretpostavka izrečena zakonom gravitacije dobro izabrana. Newton je smatrao da taj zakon vrijedi i za mehaniku na Zemlji, pa da je uzrok padanja kamena u toj općoj gravitaciji, a da on vrijedi i u nebeskim prostranstvima. Ipak, Newton nije odredio prirodu tog privlačenja budući da bi to tražilo da se postavljaju pretpostavke koje ne izlaze iz pokusa, što je on smatrao nedopustivim. Na temelju Galilejevih, Descartesovih i drugih gledišta XVII. st. formulirao je Newton načelo ustrajnosti, zatim poučak da je promjena gibanja razmjerna sili koja je proizvodi i poučak da svakoj akciji odgovara isto tolika reakcija. Ta tri poučka Newton je postavio u temelj svoje mehanike i iz njih matematički deduktivno izvodio ostale tvrdnje. Newtonova metoda je bila geometrijska i pod snažnim utjecajem Euklida. Newton je, osim tih poučaka na početak postavio svoje mehanike i nekoliko pojmova koje je definirao, kao npr. masa, veličina gibanja, sila inercije i dr., a pojmove prostora, vremena i gibanja nije definirao smatrajući ih potpuno poznatim. Prihvatio je od Giordana Bruna pojam beskonačnog prostora koji je homogen i nazivao ga apsolutnim prostorom. Vrijeme je također smatrao apsolutnim. Iako je sve tvrdnje Newton formulirao općenito, ipak je mehaniku ograničio samo na Sunčev sustav. Proširenje Newtonove mehanike na cijeli svemir izvedeno je tek u XIX. stoljeću.
Analitička mehanika. U XVIII. st. L. Euler, J. R. D’Alembert i J. L. Lagrange dali su Newtonovoj fizici analitički oblik, pa je tako došlo do tzv. analitič ke i racionalne mehanike. Ti su znanstvenici iz jedinstvenih načela izveli analitički sva područja mehanike.
G. W. Leibniz i njegovi sljedbenici bili su uvjereni
da se u prirodi ne događaju skokovi, pa su postavili tzv. zakon neprekinutosti
koji vrijedi bez iznimke u prirodi. U XVIII. st. taj je zakon doživio
brojne kritike budući da nije u skladu s mnogim iskustvenim činjenicama
(između ostaloga protivio se slučaju skoka brzine pri sudaru dviju kuglica).
Nastojanje da spasi taj zakon navelo je Dubrovčanina Ruđer
Boškovića (1711. 1787.) da dade sasvim novu teoriju o strukturi
tvari. Po toj teoriji, sila je među česticama u vrlo malim udaljenostima
odbojna, zatim nekoliko puta mijenja predznak i u većim udaljenostima
postaje privlačna. Ta su gledišta uvelike utjecala na razvoj fizike
u XIX. st.
Iako je u XVII. st. dosta prihvaćena peripatetička koncepcija širenja
svjetlosti kao vala, ipak je peripatetičko tumačenje postanka boja kao
miješanja svjetla i tame stvaralo mnoge poteškoće. Mnogi su znanstvenici
opazili da se prolaskom svjetlosti kroz prizmu dobiva niz različitih
boja. Newton je, tražeć i uzrok toj pojavi, na temelju mnogih pokusa
zaključio da je bijela svjetlost sastavljena od niza boja koje je nazvao
spektar. U XVIII. st. nije bilo moguće potvrditi koju teoriju svjetla
treba prihvatiti. Međutim, kad je Thomas Young (1773. 1829.)
oko 1800. otkrio interferenciju
svjetlosti i valove svjetlosti usporedio s valovima zvuka i valovima
vode, bila je valna teorija svjetlosti gotovo jednodušno prihvaćena.

Slika 1 Naslovna stranica Newtonovih
Principa iz godine 1687.,
u kojima je prirodna filozofija – fizika prvi put sustavno
postavljena
Grci su promatrali svijet kao cjelinu. Tako oni nisu nikada promatrali pojedini događaj ili proces izolirano od preostalog svemira. Pokusi u XVI. st. ponukali su učenjake da usredotoče svoju pozornost na konkretnu eksperimentalnu situaciju. Sve je više prevladavalo mišljenje da treba pažnju koncentrirati na mali broj okolnosti u izoliranoj situaciji. U takvom izoliranom sustavu ostajala su sačuvana neka svojstva i veličine. Descartes je govorio o očuvanju veličine gibanja, a Huygens je smatrao da je veličina mν2, gdje je m masa aνbrzina tijela, konstantna u nekom zatvorenom sustavu. Leibniz jenazivao tu veličinu živa sila.
Istraživanja toplinskih pojava. Atomistička shvaćanja u XVII. i XVIII. st. utjecala su i na predodžbe topline. Većina znanstvenika, koja je prihvaćala atomističku strukturu tvari, u to doba je zamišljala i da toplina dolazi od gibanja atomskih čestica. Daniel Bernoulli (1700. 1782.) dao je model plina na temelju pojma gibanja čestica. Uz takvo su shvaćanje pristali i Euler, Lavoisier i Laplace.
Usprkos uspjeha te teorije, došlo je u njoj i do nekih teškoća. Naime, mehanička teorija topline bila je u biti kvalitativna i nesposobna da dade neke zadovoljavajuće kvantitativne rezultate u prvoj polovini XVIII. st. Iz pokusa je izgledalo da postoji neki agens koji ne samo što djeluje na osjet opipa, a osjeća se kao temperatura tijela, nego izaziva i promjenu sastava tijela. Takav agens nađen je u okviru Descartesove prirodne filozofije. Tako je toplina shvać ena kao fluid karakterističan za toplinske procese. Ta teorija omogućila je kvantitativno mjerenje topline .

Slika 2 Naslovna stranica Boškovičeve Teorije iz
1763,
u kojoj je izložen potpuno nov pogled na materijalni
svijet i pojave u njemu
Elektricitet i atomizam materije. Elektricitet
su grčki atomisti tuma čili mehaničkim
kontaktom između objekta koje privlačeno i onog tijela koji je privučen.
Ta fizikalna veza je emisija koja potječ e od natrljanog jantara ili
od magneta. U XVI. st. je William Gilbert prihvatio tu teoriju
i zamislio da se oko natrljanog jantara ili oko magneta stvara neki
efluvij. Kao atomistička teorija topline i atomistička teorija elektriciteta,
ta je teorija zbog pokusa u XVIII. st. doživjela. modifikaciju. Za
C. F. de Cisternay du Faya (Dufay) postoje dvije
vrste elektriciteta, pa tako natrljano staklo odbija natrljano staklo,natrljani
jantar odbija natrljani jantar, a natrljano staklo privlači natrljani
jantar. On je efluvij tumačio kao vrtlog koji okružuje svaki električni
objekt. To je potaklo na mišljenje da je i elektricitet fluid. B.
Franklin je konačno prihvatio postojanje samo jednog električnog
fluida kojega može biti više ili manje od normalnog. To je omogućilo
kvantitativna mjerenja i pomoglo da C. A. Coulomb dođe do
zakona koji nosi njegovo ime.
Jedan od prvih modernih modela strukture tvari dao je John Dalton.
On je prihvatio atomistič ku strukturu tvari i zamislio da svaki atom
okružuju ljuske s atmosferom topline i tako omogućuju fizikalni kontakt
među atomima. Nove informacije o strukturi tvari pribavili su pokusi
s plinovima. Osobito su bili važni pokusi J. L. Gay-Lussaca, na
temelju kojih je Amadeo Avogadro izgradio novi model strukture
tvari. On jepretpostavio da su atomi rasuti u praznom prostoru i da
se spajaju u molekule. Na temelju postulata koji je poznat kao Avogadrov
zakon on je uspio objasniti gotovo sve kemijske rezultate poznate
u njegovo doba.
Iako je Leibniz uveo pojam žive sile koja je u biti energija, ipak
tada još nije bio poznat pojam energije uopć e. Lavoisier i Laplace
poistovjetili su toplinu s Leibnizovim pojmom žive sile, čime je uspostavljena
korespondencija između topline i mehaničke energije. Početkom XIX.
st. na temelju mnogih pokusa postalo je jasno da mora postojati neko
jedinstveno nač elo na kojemu se temelje mehaničke i toplinske pojave,
a 1842. g. Julius Robert Mayer (1814. 1878.) dokazao je da
postoji opća ekvivalencija i očuvanjesvih oblika energije. To je sve
više upozoravalo na to da bi ipak morala biti vjerojatnija pretpostavka
kinetič ke teorije topline nego fluida. Teoriju topline na temelju
gibanja čestica dao je James Prescott Joule (1818. 1889.).
Pojam polja djelovanja. Početkom XIX. st. fizičari su pretežito vjerovali da postoji neko djelovanje na daljinu i postupali su s tim pojmom čisto formalno, ne pitajući se kakav je stvarni mehanizam tog djelovanja. Na takav način bi djelovala međusobno dva naelektrizirana tijela, magneti i tijela općenito gravitacijskom silom. Ali zaobilaženje biti problema počelo je sve više smetati daljem razvoju znanosti i bilo je nužno da se pronađe upravo taj mehanizam djelovanja sile. Michael Faraday (1791. 1867.) u početku je tražio taj mehanizam u Boškovićevoj ideji središta sila. Međutim, Gilbertovi pokusi, koji su pokazali da se željezna piljevina postavlja na određene krivulje oko magneta, dopunili su tu početnu ideju. Nakon toga, Faraday je tvrdio da su magnetske crte sila realne iako nevidljive, i da one prenose međusobno djelovanje tijela. Te crte same po sebi nisu supstancija, ali nastaju zgušnjavanjem etera za koji je i Faraday uzimao da ispunja prostor i omogu ćuje zračenje ugrijanih tijela. Prostor ispunjen tim magnetskim crtama nazivao je Faraday magnetskim poljem, a isto tako prostor koji okružuje električki nabijeno tijelo elekričnim poljem.
Elektromagnetski valovi. Clerk Maxwell je našao matematički oblik za Faradayeve eksperimentalne rezultate, posebno za njegove pokuse djelovanja magnetskog polja na električno i obrnuto. Maxwell je dobio skup jednadžbi polja iz kojih je izvodio i takve rezultate koji još nisu bili provjereni eksperimentalno. Po Maxwellu, za neku dugu ravnu žicu koja vodi električnu struju postoji u okolnom prostoru tzv. elektromagnetsko polje. Ako električni naboji u žici dobivaju akceleraciju, prema Maxwellovim jednadžbama vidi se da je time odaslan u okolni prostor impuls neke energije i taj se širi brzinom svjetlosti. Ako struja u žici oscilira, valni će se niz neprekidno širiti u svim smjerovima brzinom svjetlosti. Zbog toga je Maxwell zaključio da je svjetlost elektromagnetski val.
William Herschel istraživao je (1801.) termalna svojstva spektra i utvrdio da setoplinski efekt povećava u blizini vidljivog dijela spektra. Iste je godine J. Ritter pustio da padne spektar Sunca na ploču pokrivenu srebro-nitratom i opazio da se pocrnjenje širi prema ljubičastom području spektra. Time je postalo jasno da vidljivo svjetlo predstavlja samo dio neprekidnog spektra elektromagnetskih valova. 1888. je Heinrich Hertz (1857 ...1894) pokazao da se oscilacijama iskre izmeđ u dviju kuglica spojenih na izvor struje stvara elektromagnetski val koji može proizvesti iskru između drugog para kuglica postavljenog na nekoj udaljenosti od prvih, pa je na taj način potvrdio Maxwellovu teoriju barem za frekvencije koje su različite od frekvencija vidljivog svjetla.
Poteškoće klasične fizike. Maxwellovom
teorijom klasična je fizika
dosegla svoj vrhunac. Povezana su i neka dotad različita
područja fizike: optika, elektricitet i magnetizam. S druge strane,
atomi i molekule smatrani su temeljnim dijelovima tvari. Toplina se
očituje u njihovom gibanju. Zvuk je val, a isto tako i svjetlost.
Izgledalo je da se sva podru čja fizike mogu objasniti mehanički na
temelju nekih jedinstvenih načela. Kraj XIX. st. pokazao je da to
nije tako.
Tome su prethodili neki drugi događaji. Tijekom XIX. st. znanstvenici
su se čudili kako voda u kojoj je rastopljena npr. sol vodi električnu
struju. Godine 1884. Svante Arrhenius (1859. 1927.)
pretpostavio je da postoje nabijeni atomi koje je nazvao ionima.Oni
su po njegovom mišljenju uzrok vodljivosti. Međutim, ako postoji nabijeni
atom, onda on može imati nešto više ili nešto manje tvari od neutralnog
atoma, a to se protivi pojmu atoma.
Da se riješio taj problem, pomogli su neki drugi pokusi. Otkriće Geisslerovih
cijevi postavilo je pitanje što je električna struja. William
Crookes (1832. 1919.) otkrio je da iz katode izlaze neke čestice
negativno nabijene, a te je 1891. g. G. J. Stoney nazvao elektronima.
Joseph John Thomson (1856. 1940.) zaključio je da su katodne
zrakeelektroni, koji su zajednički svim tvarima. Arrheniusovi zaključci
o ionima upućivali su na to da ti elektroni moraju biti sastavni dio
atoma. Da bi atom bio neutralan treba postojati njegov dio koji je
pozitivno nabijen. Thomson je najprije mislio da je to pozitivno nabijeni
fluid u koji su usađeni elektroni. Oscilacije tih elektrona oko ravnotežnih
položaja proizvode elektromagnetske valove. Na taj način je bilo moguće
oscilacijom elektrona u atomu objasniti mnoge pojave koje su slijedile
iz Maxwellove teorije. S druge strane, postalo je jasno da se električna
struja sastoji od elektrona, a ne od električnog fluida. Tako je,
konačno, priroda elektriciteta i struktura tvari bila međ usobno povezana.
Pored tog modela, Thomson je dao i model atoma u kojemu se elektroni
gibaju. Pretpostavio je da se elektroni gibaju oko pozitivno nabijene
jezgre. Za tu pretpostavku on primijenio je Bošković evu teoriju,
po kojoj se čestice mogu gibati samo po nekim krivuljama oko drugih.
Planetarni model strukture atoma eksperimentalno je potvrdio Ernest
Rutherford (1871. 1937.). Opravdanje uvođenja mogućih staza elektrona
dao jeNiels Bohr (1885. 1962.) . On je postulirao da sustav jezgra-elektron
normalno ne zrači energiju. Elektron prelazi s vanjske staze više
energije na unutarnju stazu niže energije, pri čemu se višak energije
emitira kao kvant elektromagnetskog zračenja .
Stefan-Boltzmannov zakon i Wienov zakon za zračenje
užarenog tijela pronađeni krajem XIX. st. potvrđivali su Maxwellovu
teoriju. Ali, usprkos tome, nije bilo moguće teorijsk izvesti oblik
krivulje koja bi prikazivala ovisnost emitirane energije i valnih
duljina o svakoj pojedinoj temperaturi. Max Planck (1858. 1947.) uvjerio
se da zračenje svjetlosti potječe od submikroskopskih električnih
oscilatora, a nakon Thomsonovih pokusa bilo je jasno da takve oscilacije
proizvode upravo elektroni. Da bi izveo relaciju koja daje raspored
emitirane energije po valnim duljinama, Planck je pretpostavio da
svaki oscilator može imati samo neku definiranu energiju i da zrači
samo onda kad on mijenja jednu dopustivu energetsku vrijednost, u
drugu manju.
Time je odstupio od načela klasične fizike. U početku, Planck nije
mogao opravdati svoju teoriju, ali je već 1905. g. Albert Einstein
pokazao da se kvantna pretpostavka mora primijeniti pri objašnjenju
fotoefekta. Novi pokusi potvrđivali su sve više Planckovu pretpostavku,
pa je time bio otvoren put kvantnoj fizici.
Još je Newton pokušao eksperimentalno dokazati postojanje apsolutnog prostora. U XIX. st. znanstvenici su pokušali identificirati apsolutni prostor s eterom i dokazati njegovo postojanje. Albert Abraham Michelson (1852. 1931.) i Edward Williams Morley (1838...1923) pokušali su to eksperimentalno dokazati, ali njihov pokus nije dokazao postojanje etera. To je navelo Alberta Einsteina da odbaci pojam etera i da postulira da u svim sustavima koji miruju ili se konstantnom brzinom gibaju vrijede isti fizikalni zakoni, i da je brzina svjetlosti u svim takvim sustavima jednaka.
To je zahtijevalo reviziju klasične fizike i uvedena je nova teorija relativnosti.
Problem zračenja užarenih tijela i Michelson-Morleyev pokus prodrmali su klasičnu fiziku i ozna čili njezinu krizu. Otkrić e elektrona i jezgre atoma (v. Atomska jezgra, TE 1, str. 479 i Subatomske čestice), kao i otkriće radioaktivnosti potakli su snažan razvoj nuklearne fizike (v. Nuklearna fizika), tako da posljednjih nekoliko desetaka godina u fizici zapravo dominira nuklearna fizika u kojoj su u činjena najvažnija otkrića i kroz koju su se otvorili najvažniji novi pogledi na materijalnu stvarnost. Ali razvoj fizike u tom razdoblju dio je naših današnjih pogleda u fizici.
4 SUVREMENA FIZIKA
Značajke suvremene fizike su sve općenitiji pogled na
prirodu i tumač enje niza pojava na osnovi nekoliko vrlo općenitih
principa, te sve veće udaljavanje od priproste intuitivne predodžbe
o svijetu.
Početkom XX. stoljeća usporedno se razvijaju teorija relativnosti
i kvantna fizika, jedna kao konačna razrada Maxwellove elektrodinamike,
a druga kao posljedica nastojanja da se klasična mehanika i elektrodinamika
prošire na opisivanje atomske građe tvari.

Slika 3 Shematski prikaz međusobnog
utjecaja fizikalnih teorija
te njihov utjecaj na glavna područja primjene
Transformacijska invarijantnost. U svojoj sintezi, još u renesansi započete revolucije u znanosti, I. Newton je naglasio značenje kvantitativnih mjerenja, spoznavanja zašto se stvari događaju kroz opis kako se one događaju, odbacuju ći aristotelovske moralno-etičke antropomorfne atribute kao irelevantne za tvarni svijet. U novom gledanju, koje je u povijesti ljudskog umnog razvoja isto toliko važno kao i starogrčki skok od empiričke geometrije starih Egipćana i Babilonaca do logički sazdane euklidske matematičke zgrade, važni su analitički geometrijski koordinatni sustavi (R. Descartes, 1637.). Objektivne prirodne pojave ne mogu ovisiti o samovoljno odabranom koordinatnom sustavu za njihovo matematičko opisivanje. U suvremenoj su teorijskoj fizici proučavanja ponašanja teorijskih izraza pri promjenama koordinatnih sustava, tzv. transformacijska invarijantnost, neobično važne. Te invarijantnosti mogu se povezati sa sačuvanjem fizikalnih veličina (E. Nother, 1918.). Tako, npr., invarijantnosti pri translaciji sustava, tj. sloboda u izboru početka koordinatnih osi, znači u četverodimenzionalnom vremenu-prostoru sačuvanje energije i impulsa. Ta fizikalna relativnost izbora koordinatnog sustava dala je ime teoriji relativnosti. Još krajem XIX. stoljeća spoznato je da Maxwellove jednadžbe. mijenjaju svoj oblik pri jednolikom gibanju koordinatnog sustava ako se pri tome vrijeme smatra apsolutnim i nepromjenljivim. Newtonove jednadžbe su s obzirom na takve transformacije nepromjenljive. Međutim, sva nastojanja da se djelovanje promjena u elektrodinamičkim sustavima zbog jednolikoga gibanja izmjere (najosjetljiviji tadanji pokus bio je već spomenuti Michelson -Morleyev pokus) bila su bezuspješna. Proučavajući sustave u gibanju, H. A. Lorentz je 1899. i 1903. godine ustanovio da Maxwellove jednadžbe ostaju nepromijenjene uvede li se transformacija vremena, koja vodi na neko drugo vrijeme koje je Lorentz nazvao lokalnim vrijemenom. Te Lorentzove transformacije, čije je potpuno fizikalno značenje spoznao nešto kasnije A. Einstein, važna su sastojina moderne fizike. Maxwellova teorija izvanredno je empirički opravdana, u njoj je sadržano stoljetno iskustvo o elektromagnetizmu i sastavni je dio naše tehnologije i industrijskih primjena. Isto, naravno, vrijedi i za zakone klasične mehanike. Bilo je zbog toga vrlo neobično kada se krajem prošlog i početkom ovog stoljeća činilo da su elektromagnetski i svjetlosni fenomeni u suprotnosti s mehaničkim zakonima. Poznati matematičar H. Poincare posumnjao je u valjanost klasične mehanike (1904.), nagađajući da će se razviti nova vrsta dinamike kod koje će najveća moguća brzina biti brzina svjetlosti. U svom fundamentalnom radu (1905.) A. Einstein je analizirao pojam istodobnosti koji je bitan za mjerenje vremena. Pokazao je da se istodobnost može ustanoviti samo slanjem signala izme đu opaža ča, te da ovisi o najbržem mogućem posredniku, a to je svjetlost. Uzme li se da je brzina svjetlosti u svim koordinatnim sustavima jednaka, dobiju se za prijelaz od sustava na sustav Lorentzove transformacije. Time su protumačeni negativni rezultati Michelson-Morleyevog i drugih sličnih pokusa. Pojava dužinske kontrakcije (G. F. Fitzgerald, 1892.) i dilatacije vremenskog razmaka (Larmor, 1900.), koje su stariji istraživači pripisivali elektromagnetskim pojavama u tvari, posljedica su načina mjerenja, koje je određeno fizikalnim silama i zakonima. Newtonovske jednadžbe mehanike moraju se modificirati, no odstupanja od klasične fizike postaju značajna tek pri vrlo velikim brzinama, bližim brzini svjetlosti. Kako se elektromagnetske pojave odvijaju brzinom svjetlosti, u Maxwellovim jednadžbama mjerenje vremena je i nesvjesno bilo uključeno na relativistički način i te jednadžbe su relativističke. Modifikacije mehanike nevažne su u svakidašnjem životu, no one postaju važne već pri konstrukciji elektroničkih uređaja. Već je 1901. W. Kaufmann primijetio da se gibanje vrlo brzih elektrona može opisati klasičnom mehanikom samo ako se dopusti porast mase s brzinom. Specijalna teorija relativnosti, sinteza klasične mehanike i elektrodinamike, bez poteško ća opisuje sve takve pojave. Njena valjanost je dokazana i svakodnevno se dokazuje u tvornicama i laboratorijima diljem svijeta. Rad velikih i moćnih akceleratora elementarnih čestica i pojave koje se s njima proučavaju u potpunom su skladu s teorijom relativnosti i mogu se samo kroz nju sustavno spoznati. Poznato je npr. da brze nestabilne čestice postoje (“žive”) duže od jednakih mirnih čestica, kako to i traži relativistička dilatacija vremena. (B. Rossi i D. B. Hall, 1941.). Prema jednoj procjeni 1963. je u SAD-u valjanost euklidske geometrije na kojoj se osniva klasična mehanika ispitana pri geodetskim mjerenjima bar 840.000 puta s točnošću od barema 10-5. Istovremeno je pri radu akceleratora elementarnih čestica ispravnost Lorentzovih transformacija, koje su osnova teorije relativnosti, dokazana barem milijun puta s jednakom ili većom točnošću. Danas se više i ne govori o specijalnoj teoriji relativnosti kao o posebnoj fizikalnoj teoriji. Zahtjev relativističke invarijantnosti, tj. nepromjenljivosti teorije prema Lorentzovim transformacijama, ugrađen je u sve fizikalne teorije, pa i u kvantnu mehaniku.
KVANTNA MEHANIKA . Ta se disciplina
razvila u nešto više od jednog desetljeća nakon Bohrovog
izvoda vrijednosti Rydbergove konstante (J. R. Rydberg, 1890., N.
Bohr, 1913.) i tumačenja Balmerove serije (J. J. Balmer, 1885.) atomskih
spektara. Važne doprinose Bohrovoj teoriji dao je A. J. W. Sommerfeld
(1915.), koji je pokazao kako se ona može poopćiti na slučaj elipti
čkih staza elektrona, te protumačio hiperfinu strukturu spektralnih
linija kao relativističku pojavu.
Proučavajući srazove elektrona i atoma, J. Frank i G.
Hertz su 1914. pokazali da se i pri tom procesu predaja energije
zbiva u skokovima. Niz pojava u vezi s atomima, njihovim spektrima
i drugim svojstvima, počelo se kvalitativno, a ponekad i kvantitativno
razumijevati. No tumač enje fine strukture spektara alkalijskih metala
ili Zeemanovog efekta nije bilo moguće u okvirima jednostavne Bohrove
teorije. Zeemanova pojava (P. Zeeman, 1896.), da se pri zračenju atoma
u snažnom magnetskom polju spektralne linije dijele, bila je važan
korak, uz Rutherfordov rad, za shvaćanje da i atomi imaju neku strukturu
(H. A. Lorentz, 1897.). Ključ za tumačenje rezultat je opažanja da
se rojevi atoma pri prijelazu kroz nehomogeno magnetsko polje dijele
u nekoliko komponenata. Moralo se zaključiti da elektron nosi svoj
vlastiti impulsni moment, tzv. spin (G. F. Uhlenbeck i S. Goudsmit,
1925.), koji bi u naivnoj slici sličnoj planetarnom sustavu bio analogan
okretanju planeta oko vlastite osi. Spin je pomogao W. Pauliju (1924.)
pri formulaciji znamenitog principa isključenja, koji kaže da u atomu
niti dva elektrona ne mogu biti u istom kvantnom stanju. Na osnovi
principa isključenja, elektroni postupno pune atomske staze, tako
da u svakoj može biti određen broj, pa se jedino tako mogu shvatiti
atomski spektri i periodni sustav elemenata . Pri proučavanju nakupina
čestica ili atoma metodama statističke fizike primijećeno je da postoje
dvije statistike: za čestice s polovičnim spinovima, kao što je elektron,
vrijedi princip isključenja (E. Fermi, 1926.), dok za čestice s cijelim
spinovima ne vrijedi (S. N. Bose, 1924., A. Einstein, 1924.). Do sredine
dvadesetih godina razvijena stara kvantna teorija bila je još puna
formalnih proturječnosti i nekonzistentnosti. U njoj su na klasičnu
elektrodinamiku i mehaniku bili nadodani kvantni postulati, što se
opravdalo empiričkim uspjehom. No, dok je tu predviđanje rasporeda
spektralnih linija po frekvencijama bilo izvrsno, teorija je tek s
velikim poteškoćama mogla nagađati o jakosti ili intenzitetu dane
spektralne linije. Valna svojstva svjetlosti, ogib i interferencija
nisu se mogli povezati sa svjetlosnim česticama, fotonima, koji se
gibaju prostorom kao puščana tanad, što je slijedilo iz Einsteinovog
opisivanja fotoefekta. Izučavajući
sudare fotona i elektrona A. H. Compton (1923.) našao je zakone slične
sudarima materijalnih objekata. Budući da se radilo o velikim brzinama,
pri proračunu je upotrijebljena relativistička formulacija mehanike,
a svjetlost je shvaćena kao roj fotona.
Valovi materije. Daljnji razvoj kvantne teorije učinio je taj dualizam val-čestica manje zabrinjavajućim. Potaknuti L. de Broglievim spekulacijama (1923.) o valovima materije , više je fizičara pokazalo (W. Elsasser 1925.; C. J. Davisson i C. H. Kunsman 1925.; C. J. Davisson i L. H. Germer 1927.; G. P. Thomson 1927.) da se elektron pri raspršenju na vrlo finoj kristalnoj rešetki giba baš kao i svjetlost. W. Heisenberg je 1925. u nastojanju da opiše atomske spektre, upotrebljavajući samo fizikalno mjerljive amplitude povezane s jakošću spektralnih linija, postavio algebarski sustav jednadžbi. Ta teorija, razrađena kasnije (M. Born, W. Heisenberg i P. Jordan 1926.; P. A. Dirac 1925.) u kvantnu mehaniku (temeljenu na formalizmu nekomutativnih operatora) mogla je na matematički konzistentan i fizikalno potpun način opisati kvantne fenomene. Ubrzo poslije toga, F. Schrodinger je (1935.), nadovezujući se na de Broglieve ideje i na sličnost između klasične mehanike i geometrijske optike (W. R. Hamilton, 1934.), konstruirao svoju valnu mehaniku u analogiji s valnom teorijom svjetlosti. Schrodinger je uskoro pokazao matematičku ekvivalentnost između svoje valne mehanike i Heisenbergove kvantne mehanike. Danas se govori o kvantnoj mehanici prema Schrodingerovom ili prema Heisenbergovom prikazu, te je svaki od njih pogodan za određene primjene. Nerelativistička verzija kvantne mehanike bila je bitna pri otkrivanju poluvodiča i izuma lasera, te polako već ulazi u tehničke primjene. Dopunjena spoznajom o elektronskom spinu dovoljna je za potpuno shvaćanje periodnog sustava elemenata i za opisivanje molekula i kemijskih reakcija. Njenim primjenama na sustave s više čestica razvile su se discipline: atomska fizika, fizika čvrstog stanja, molekularna fizika, kvantna kemija, nuklearna fizika i sl.
Statistička interpretacija kvantne mehanike. Proučavanje strukture kvantne mehanike i njene fizikalne interpretacije veoma je izmijenilo je predodžbe o načinu na koji se spoznaje materijalni svijet. Pokazalo se (M. Born, 1926.) da teorija daje samo statističke informacije o vjerojatnosti zbivanja nekog događaja. Pri raspršenju elektrona na kristalnoj rešetki, teorija ne može predvidjeti ponašanje pojedinog elektrona, nego samo kaže kolika je vjerojatnost da se elektron negdje nađe. Ponovili se eksperiment za mnogo elektrona, statistička distribucija odgovara ogibnoj valnoj slici, pa je tako problem dualizma val-čestica razriješen. Statistička interpretacija kvantne mehanike bitno je različita od klasič ne statistike, gdje je statističko ponašanje posljedica toga što nema točnih informacija o svakoj čestici u mnoštvu, iako se te informacije, u načelu, mogu saznati. U kvantnoj se mehanici ne mogu u načelu dobiti potpune informacije o danoj čestici, što je formulirano kroz znamenito načelo neodređenosti (W. Heisenberg, 1927.). Impuls i položaj elektrona npr. ne mogu se istodobno po volji točno izmjeriti. Ako je položaj apsolutno poznat, impuls je neodređen i obrnuto. Promatranje nekoga fizikalnog sustava znači međudjelovanje sustava s nekim mjernim instrumentom. Po predodžbama klasične fizike, takvo se međudjelovanje zbiva kontinuirano. Može se, dakle, po volji smanjiti, toliko da postane nevažno. No, kod kvantne mehanike samo postojanje kvantnih skokova ograničava mogućnost da se takvo međudjelovanje potpuno reducira. Načelo neodređenosti je mnogo puta eksperimentalno verificirano. Osobito je uvjerljivo mjerenje kod nuklearnih raspada, gdje se pokazuje da sve točnije određenje poluživota dovodi do sve veće netočnosti u određivanju energije emitiranog zračenja. Napuštanje jednostavnog determinističkog shvaćanja fizike protivi se, naravno, našem svakidašnjem iskustvu, zasnovanom na vizualnim i čulnim opažanjima pojava pri kojima su kvantni fenomeni nevažni. Kod atomskih i subatomskih pojava radi se obično o obilju događaja, pa se ta točnost statističkog predviđanja, kao npr. ogibne slike, može testirati izvanredno precizno, često mnogo točnije od mjerenja karakterističnih za klasičnu fiziku iz prošlog stoljeća. Mnogobrojna nastojanja da se ipak razvije deterministička slika kvantnih pojava bila su do sada potpuno bezuspješna. To je 1959. potaklo D. Bohma i Y. Aharonova da nač ine pokus koji je pokazao da i elektromagnetski potencijal (dakle nefizikalna veličina u klasičnoj fizici koja poznaje samo polja) i u situaciji u kojoj je polje isključeno utječe na ogib elektrona. To je sasvim u skladu s kvantnomehaničkim jednadžbama.
Stvaranje i nestajanje čestica. Iako vrlo uspješna i u sebi potpuno konzistentna teorija, kvantna mehanika, određena Heisenbergovim hamiltonijama i Schrodingerovom jednadžbom, ne opisuje sve prirodne fenomene. Ta formulacija nema relativističku invarijantnost. U kvantnoj mehanici uzima se da je broj čestica konstantan pa nema mogućnosti da se opiše čin spontane emisije svjetlosti, koji znači stvaranje nove čestice, fotona. Sličnost s klasič nom teorijom elektromagnetizma omogućavala je da se emisija fotona proračuna, no to nije zadovoljavalo potrebu za jasnoćom i skladnošću fizikalne teorije. Želeći ukloniti tu nedorečenost i nepotpunost P. A. M. Dirac je, upotrebljavajući analogiju s harmoničkim oscilatorom, kvantizirao elektromagnetske valove. Njegov je rad jedno od važnih znanstvenih dostignuća u prošlom stoljeću, budući da se u njemu prvi put poslije tisuća godina postojanja atomističkih teorija pojavljuje mogućnost da je broj elementarnih djelića materije promjenljiv. Diracov rad nadovezuje se na dugi razvoj. Započeo ga je J. W. Rayleigh 1900. kada je pri izvodu klasične teorije užarenog tijela promatrao svjetlosne titraje u prostoru kao statistički sustav harmoničkih oscilatora. Već 1906. je P. Ehrenfest predlagao da se Planckova kvantizacija oscilatora u tijelima koja zrače proširi i na zamišljene oscilatore elektromagnetskog polja. To je omogućilo P. Debyeu da 1910. izvede Planckov zakon zračenja. No prava veza s Einsteinovim česticama svjetlosti dugo nije bila shvaćena. Tek 1926. su M. Born, W. Heisenberg i P. Jordan uočili matematičku ekvivalentnost Debyevog pristupa s Einstein-Boseovom kvantnom statističkom teorijom plinova. Jer ako kvantizacija Rayleighovih oscilatora daje isti rezultat kao teorija koja opisuje mnoštvo čestica nekog plina, onda su ti kvantizirani valovi zapravo svjetlosne čestice. Diracova uspješna formulacija tih ideja još uvijek nije vodila na skladnu i simetričnu teoriju međudjelovanja elektrona i fotona. Heisenbergova i Schrodingerova kvantna teorija odgovarala je zapravo nekvantiziranim Maxwellovim jednadžbama. Osim toga teorija fotona bila je, automatski, i relativistički invarijantna.
Materija i antimaterija. Još je Schrodinger pokušao povezati čestice i valove na relativistički način. Primjenjujući takvu teoriju na vodikov atom, primijetio je da se ne slaže s pokusima. Međutim, nerelativistička aproksimacija, tj. znamenita Schrodingerova jednadžba, koju je posljednju objavio, bila je točnija. Kasnije je i primijećeno da se relativistička verzija teorije ne može interpretirati u smislu Bornovih vjerojatnosti. Razrješenje obaju problema poteklo je 1928. od P. A. M. Diraca, koji je u teoriju uveo spinore. Pokazalo se da postoji više relativističkih verzija Schrodingerove teorije te da prvotna Schrodingerova relativistička jednadžba (poznata u fizici po kasnijim istraživačima kao Klein-Gordonova jednadžba) opisuje čestice bez spina. Elektroni, čestice spina ½, opisani su Diracovom jednadžbom, čija su rješenja u potpunom skladu s finom strukturom atomskih spektara. No uz ta rješenja Diracove jednadžbe pojavila su se rješenja koja bi formalno odgovarala česticama negativnih energija, što je očito bilo besmisleno. Dirac je ta “suvišna” rješenja pokušao pripisati nekim novim česticama različitim od elektrona. Znanstvenici su ubrzo spoznali da bi ta dodatna rješenja mogla odgovarati čestici pozitivne energije koja ima istu masu kao elektron, no suprotni električni naboj. Proučavajući u Wilsonovoj komori (C. T. R. Wilson, 1897.) putanje čestica stvorenih kozmičkim zračenjem, C. D. Anderson otkriva 1932. pozitron ili pozitivni elektron, koji ima svojstva baš kao što ih je teorija i predvidjela. Andersonov pokus, pri kojem je visokoenergetski proton pogodio atomsku jezgru stvorivši par elektron-pozitron, rezultirao je i bitno novom spoznajom. Nisu samo fotoni č estice koje u prirodi mogu nastajati i nestajati, nego to vrijedi za kvante ostalih polja, tj. za elementarne čestice. U suvremenu teoriju polja pozitron je ugrađen potpuno simetrično s elektronom (P. Jordan i E. Wigner, 1928.; W. Heisenberg i W. Pauli, 1929., E. Fermi, 1930.), on je njegova antičestica. U teoriji polja i materija (čestica) i antimaterija (antičestica) promatraju se na potpuno simetričan način. O izboru je ovisno što će se nazvati materijom, a što antimaterijom. U kvantnoj teoriji polja elektroni, fotoni i druge elementarne čestice opisuju se na ravnopravan način te u njoj više nema proturječ ja val-čestica. Tako je Diracovo otkriće čestica i antič estica potpuno izmijenilo pogled na fiziku. Do toga su doba elementarne čestice zamišljane u duhu antičke Demokritove filozofije kao najmanji djelići tvari koji se nikada ne promijene i nikada se ne mogu pretvoriti u nešto drugo. Starodrevni antički problem dijeljenja materije osvijetljen je sada na nov način. Prirodi ne odgovara ni jedna od dviju naivnih logičkih mogućnosti: da se materija ili može beskonačno dijeliti u sve manje i manje djeliće ili da se mora jednom doći do najmanjih mogućih č estica. Relativistič ka povezanost mase i energije (A. Einestein, 1906.) znači u teoriji polja mogućnost stvaranja čestica iz energije. Foton dovoljno visoke energije može se u nedogled dijeliti u sve nove i nove parove čestica-antičestica. Pljuskovi čestica zapaženi najprije u kozmi čkom zračenju stvaraju se i proučavaju svakodnevno pri akceleratorskim eksperimentima.
koje se otkrilo u svijetu elementarnih čestica bio je potpun uspjeh kvantne teorije
Uspjesi i poteškoće suvremene fizike. Mnogi drugi uspjesi koji su slijedili nisu bili tako potpuni, ostavljajući ili neke nedorečenosti ili zahtijevajući uvođenje semiempiričkih pretpostavki. Kvantna teorija, kao uostalom i sve teorije prije, nailazi na velike poteškoće pri opisivanju problema mnogih tijela. Oslanjajući proračunske aproksimacije na eksperimentalne podatke, moglo se postići shvaćanje supravodljivosti (H. Frohlich, 1950., J. Bardeen, L. N. Cooper i J. R. Schriffer, 1957.), suprafluidnosti (L. D. Landau, 1941.), razumjeti svojstva poluvodiča i predvidjeti mogućnost konstrukcije tranzistora (J. Bardeen i W. Shockley, 1946.). Shvaćena su mnoga svojstva strukture atomske jezgre (W. Heisenberg, 1932., N. Bohr, 1936.; M. G. Mayer, 1948., J. H. D. Jensen, 1949., A. Bohr iB. Mottelson, 1953.), iako su tu svi uspješni pristupi nužno poluempirički zbog nedovoljnog poznavanja prave prirode nuklearnih sila. Poteškoće su povezane s još vrlo površnim razumijevanjem svijeta elementarnih čestica s jedne strane i sa stanjem u kvantnoj teoriji polja, s druge strane. U poratnim godinama završena je formulacija računa smetnje u kvantnoj elektrodinamici (R. P. Feynman, 1949., J. Schwinger, 1948., S. Tomonaga, 1948., F. Dyson, 1949.) . Nađena je mogućnost uklanjanja beskonač nosti koje se pojavljuju pri proračunima kroz postupak renormalizacije (H. A. Kramers, 1938.). Iako je moguće konstruirati formulaciju teorije u kojoj se beskonačnosti ne pojavljuju (tzv. postupak LZS), među znanstvenicima postoji čvrsto uvjerenje da još uvijek nije postignuto potpuno razumijevanje. Kvantna elektrodinamika uspjela je objasniti mala odstupanja u vodikovom spektru (W. E. Lamb i R. C. Retherford, 1947.; H. A. Bethe, 1948.) te anomalnu veličinu magnetskog momenta elektrona (H. M. Foley i P. Kush, 1947., J. Schwinger, 1949.). Ni jedan od tih fenomena nije se mogao shvatiti u kvantnoj mehanici, gdje se ostalo na razini u kojoj nije u teoriju uključena mogućnost stvaranja i nestajanja čestica. U jeziku kvantne elektrodinamike fizikalni foton uključuje u sebi i bezbrojne virtualne parove elektron-pozitron, dok je elektron također okružen virtualnim fotonima i parovima, sve u neprekidnom međudjelovanju. Mnogobrojni pokusi u kojima se proučava međudjelovanje elektrona i fotona nisu još otkrili nikakvo neslaganje s kvantno-elektrodinamičkim teoritskim opisom, iako je već postignuta toč nost od jedne desettisuć inke od 1%. To je dovelo do nastojanja da se ideje kvantne teorije polja primijene i na druge procese. Njena relativistička verzija bila je bitna za razumijevanje već spomenutih mnogočestičnih fenomena. Važan sastojak današnje fizike su tzv. Feynmanovi dijagrami, slikoviti prikaz fizikalnih procesa u obliku simboličkog crteža kojemu se po jednostavnim pravilima mogu pridruživati odgovaraju ći matematički izrazi. Isto je tako koristan i pojam S -matrice (W. Heisenberg, 1943.). Ta formulacija teorije želi raditi samo s eksperimentalno mjerljivim velič inama te se u njoj o čituje uzročna povezanost fizikalnih događaja. Kvantna teorija polja je jezik koji moderna znanost upotrebljava u opisivanju i proučavanju elementarnih čestica. Već 1935. je H. Yukawa zaključio da kratki doseg nuklearnih sila upozorava na postojanje nove elementarne čestice, piona (C. M. G. Lattes, H. Muirhead, G. P. S. Occhialini i C. F. Powell, 1947.), kojoj je mogao predvidjeti i masu. No, zamršeni nelinearni sustav operatorskih jednadžbi kvantne teorije polja dopušta aproksimativna rješenja samo za sluč aj dovoljno slabih međudjelovanja (elektrodinamika, slabe interakcije). Nesposobnost da se problem potpuno i dinami čki riješi naglašava važnost proučavanja simetrija međ u elementarnim česticama. Otkriće izotopnog spina (W. Heisenberg, 1932.), kvatnog broja stranosti (K. Nishijina, 1953M. Gell-M., ann, 1953.) i tzv. SU (3) simetrije (Y. Neeman 1961.; M. Gell-Mann 1961.) te izučavanje općih zakona sačuvanja fizikalnih veličina, omogu ćilo je da se teoritski unaprijed predvidi postojanje mnogih novih čestica. Slično je u prošlom stoljeću Mendeljejevljev periodni sustav elemenata upozorio na postojanje do tada nepoznatih elemenata. No, svijet elementarnih čestica još uvijek nije uhvaćen u teoretske teme jer se neprestano otkrivaju nove neslućene čestice i nova neočekivana svojstva. Uz neočuvanje pariteta (tj. slabo međudjelovanje je u prostoru orijentirano; T. D. Lee i C. N. Yang 1956.), otkrivena je i zagonetna vremenska neobrativost nekih slabih procesa (raspad K° mezona, 1964.). Uporaba sve moćnijih i moćnijih akceleratora znači promatranje tvari pod sve već im i većim pove ćanjem (u Hamiltonovom smislu tu postoji potpuna analogija s optičkim mikroskopom), u nadi da će se otkriti nešto novo, kao što se to do sada i događalo. Ima znakova da i subatomske čestice, protoni, pokazuju neku strukturu kada se promatraju pod snopom elektrona vrlo visoke energije (kratka valna duljina, silno povećanje), baš kao što je nekada i atom pokazao strukturu, kada ju je Rutherford “osvijetlio” snopom α-čestica. No poteškoće, nepotpunosti i nedorečenosti u razumijevanju prirode dopuštaju da se ozbiljno postavi pitanje nije li pragmatična metoda (oslanjanje na početne, općevrijedne zakonitosti) u fizici, kako ju je definitivno uobličio Newton, istrajala svoj vijek? Pokušaji stvaranja jedinstvene osnovne teorije prirode (W. Heisenberg, 1954.) daleko su još od uspjeha. Gravitacija, koja je od osnovne važnosti u astronomskim i kozmič kim razmjerima, zanemaruje se u atomskoj i subatomskoj fizici kao izvanredno slabo međudjelovanje. Postoje ipak zanimljiva dodirna područja. Posljedica Einsteinovog principa ekvivalencije (A. Einstein 1907., 1911.), predviđena promjena valne duljine (energije) elektromagnetskog zračenja u jakom gravitacijskom polju, testirana je i u laboratoriju na Zemlji. Mossbauerovo otkriće (R. L. Mossbauer, 1957.) da foton emitiran jezgrom koji je dio čvrstog tijela ne gubi energiju zbog odboja, omogućava izvanredno precizno mjerenje energije elektromagnetskog zračenja. Mogao se izmjeriti porast u energiji fotona koji pada u zemaljskom gravitacijskom polju (R. V. Pound i J. L. Snider, 1965.). Sinteza neeuklidske geometrije gravitacije u općoj teoriji gravitacije (A. Einstein, 1913.) prisutna je kod mnogih spekulacija u suvremenoj astrofizici, kao što je na primjer nagađanje da bi neobične pulsirajuće zvijezde (“pulsars”, Sveučilište u Cambridgeu, 1967.) mogle biti još odavno predviđene neutronske zvijezde (L. D. Landau, 1934; T. Gold 1968.).

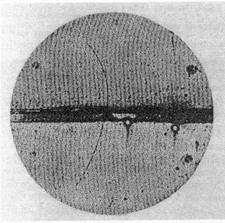
Slika 5 Snimke maglene komore koje pokazuju antihilaciju protona i anatiprotona u pione. Glavni događaj je u sredini slike. Antiproton upada odozgo i njegov je trag gotovo ravan. Pri antihilaciji je stvoreno osam piona. Jedan od njih, koji je gotovo suprotno usmjeren od upadnog antiprotona, raspada se na mion i neutrino. Mion se nadalje raspada na pozitron i dva neutrina. Trag miona je oštar za razliku od traga piona, a početak traga pozitrona se jasno vidi. Komora je smještena u magnetskom polju okomitom na ravninu slike. Tragovi negativnih čestica zakreću se u smjeru kazaljke na satu, a tragovi pozitivnih čestica u obratnom smjeru. Sporije čestice ostavljaju gušće, a brže isprekidane tragove
Tendencije razvoja. Suvremena fizika je daleko od sigurnosti tzv. klasične fizike iz sedamdesetih godina devetnaestog stoljeća, kada se za jedan kratki trenutak činilo da su gotovo već dokučene i posljednje tajne svijeta. Obilje eksperimentalno-teorijskih spoznaja, od kojih su u ovom prikazu mogle samo neke biti ilustrativno navedene, pokazuje da se iako se dosta dobro razumije svijet atoma, u svijet još manjih dimenzija tek se zakoračilo. Fizika u svom eksperimentalno-materijalističkom pristupu izučavanja svijeta nije definicijsko učenje. U njenoj se znanstvenoj metodi želi razumjeti i ustrojstvo i rad mehanizma svijeta, kako bi se on čovječjom voljom mogao iskoristiti i kako bi se moglo na njega utjecati. U tom smislu ova pustolovina ljudskog duha koja se naziva fizikom začela se još s prvom vatrom pračovjeka.
preuzmi
seminarski rad u wordu » » »


